SciPy - integrate.romb() Method

The SciPy integrate.romb() method is used to perform the task of numerical or romberg integration. This method also helps us to plot the graph based on sample/coordinates points.

Syntax

Following is the syntax of the SciPy integrate.romb() method −

romb(y, dx = int_val/float_val/1.0)

Parameters

This function accepts the following parameter −

• y: This parameter determine the array function which valued at discrete points and these points consider even spaces.
• dx: This parameter determine the spacing between the points and default value is 1.0 if not specify.

Return value

This method return the estimate value of type float.

Example 1

Following is the SciPy integrate.romb() method that shows the simple integration function f(x) = x² over the interval between 0 and 1. The resultant value based on five discrete point.

import numpy as np
from scipy import integrate

# define the function values at discrete points
x = np.linspace(0, 1, 5)
y = x**2 

# calculate the integral
res_integral = integrate.romb(y, dx=x[1] - x[0])

# display the result
print(res_integral)

Output

The above code produces the following result −

0.3333333333333333

Example 2

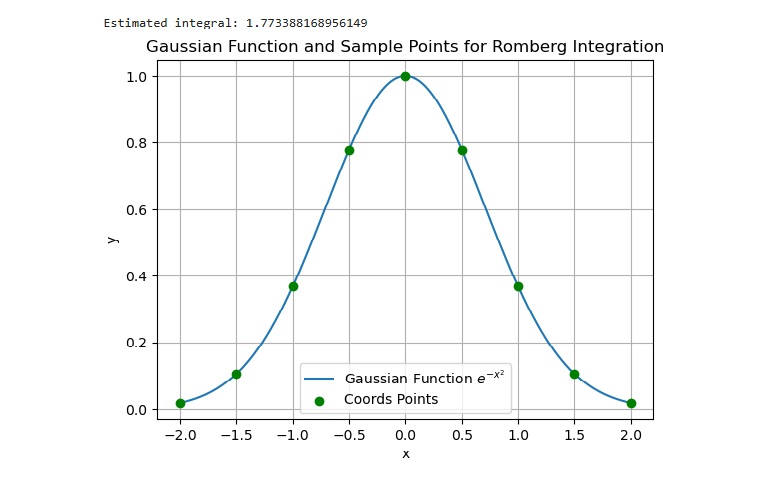
This program demonstrate the numerical integration of Gaussian function which is e^-x2 over the interval between -2 to 2 and the function values are represented as nine points(x-axis).

import numpy as np
from scipy.integrate import romb
import matplotlib.pyplot as plt

# define the function values at discrete points
x = np.linspace(-2, 2, 9)
y = np.exp(-x**2)

# calculate the integral
res_integral = romb(y, dx=x[1] - x[0])

# display the result
print(f"Estimated integral: {res_integral}")

# plot the Gaussian function and the points used in Romberg integration
x_fine = np.linspace(-2, 2, 1000)
y_fine = np.exp(-x_fine**2)

plt.plot(x_fine, y_fine, label='Gaussian Function $e^{-x^2}$')
plt.scatter(x, y, color='green', zorder=5, label='coords Points')

plt.title('Gaussian Function and Sample Points for Romberg Integration')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

Output

The above code produces the following result −