SciPy - stats.norm.ppf() Function

---

---

scipy.stats.norm.ppf() is a function in the SciPy library that computes the percent-point function (PPF), also known as the inverse cumulative distribution function (Inverse CDF), of a normal distribution. This function is useful for finding the value of x corresponding to a given cumulative probability. It is part of SciPys stats module where loc represents the mean () and scale is the standard deviation ().

The percent-point function is mathematically defined as the inverse of the cumulative distribution function (CDF):

$\mathrm{x = F^{-1}(p)}$

where:

• F(x) is the cumulative distribution function (CDF).
• p is the given cumulative probability.
• F(p) is the inverse CDF (percent-point function).

Syntax

Following is the syntax for using scipy.stats.norm.ppf() which is used to compute inverse percent-point function −

scipy.stats.norm.ppf(q, loc=0, scale=1)

Parameters

Below are the parameters of the function scipy.stats.norm.ppf() −

• q: The cumulative probability (quantile) for which the corresponding x value is computed.
• loc (optional): The mean () of the normal distribution. Default value is 0.
• scale (optional): The standard deviation () of the normal distribution. Default value is 1.

Return Value

This function returns the x value corresponding to the given cumulative probability q in a normal distribution.

Computing the 50th Percentile (Median)

The 50th percentile (median) of a standard normal distribution is mean = 0 and standard deviation = 1. This can be computed using scipy.stats.norm.ppf() −

from scipy.stats import norm

q = 0.5  # 50th percentile
x_value = norm.ppf(q, loc=0, scale=1)

print(f"Value at the 50th percentile: {x_value}")

Below is the output of computing 50th percentile −

Value at the 50th percentile: 0.0

Computing the 95th Percentile

For a normal distribution with mean = 100 and standard deviation = 15 the 95th percentile can be calculated with the help of below example −

from scipy.stats import norm

q = 0.95
x_value = norm.ppf(q, loc=100, scale=15)

print(f"Value at the 95th percentile: {x_value}")

Here is the output of the computing the 95th Percentile −

Value at the 95th percentile: 124.67280440427209

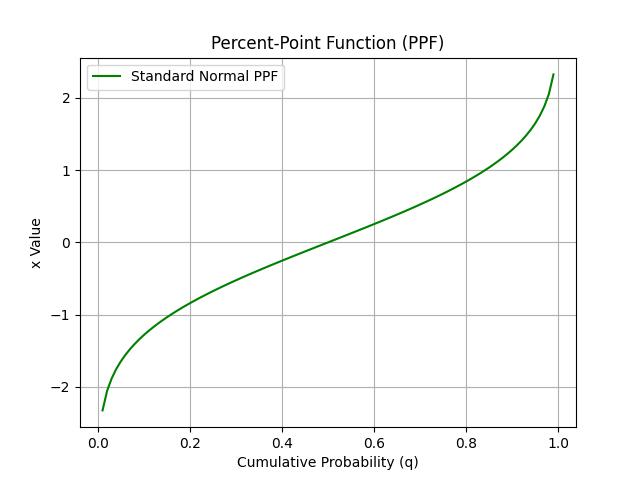
Plotting the Inverse CDF (PPF)

The percent-point function (PPF) maps cumulative probabilities to x values. Below is a plot of the PPF for a standard normal distribution −

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

q_values = np.linspace(0.01, 0.99, 100)
x_values = norm.ppf(q_values, loc=0, scale=1)

plt.plot(q_values, x_values, label="Standard Normal PPF", color="green")
plt.title("Percent-Point Function (PPF)")
plt.xlabel("Cumulative Probability (q)")
plt.ylabel("x Value")
plt.legend()
plt.grid(True)
plt.show()

Below is the output plot of the Inverse CDF i.e., PPF −

Finding the 10th Percentile

In this example, we compute the 10th percentile for a normal distribution with mean = 50 and standard deviation = 10 −

from scipy.stats import norm

q = 0.10
x_value = norm.ppf(q, loc=50, scale=10)

print(f"Value at the 10th percentile: {x_value}")

Here is the output of computing the 10th Percentile −

Value at the 10th percentile: 37.184484344553994