Injective Functions in Automata Theory

---

---

Read this chapter to understand the concept of one-to-one functions in automata theory. One-to-one functions are also known as injective functions. These functions play an important role in Set Theory too. We will see their definitions with examples and their properties for a better understanding.

One-to-One (Injective) Function

A one-to-one function, also called an injective function, is a function that maps elements from one set, say Set A, to another set, Set B, in such a way that no two elements in Set A map to the same element in Set B. This means that each element of Set A has a unique image in Set B.

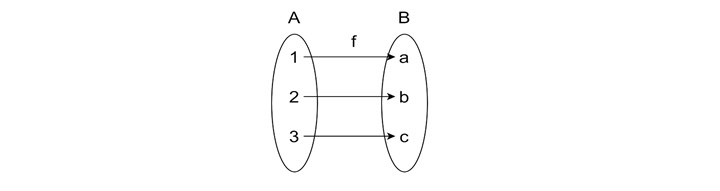
Here, A contains {1, 2, 3} and B contains {a, b, c} the function is like the above figure and it is one to one function.

Let us see another example which is not one-to-one.

• Set A contains three elements: {1, 2, 3}.
• Set B contains two elements: {A, B}.

Let's map the elements from Set A to Set B −

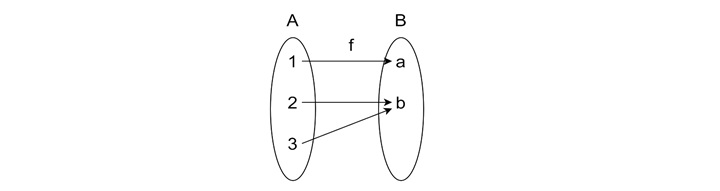
This is not a one-to-one function because both 2 and 3 map to B. In a one-to-one function, each element of Set A must map to a unique element in Set B. Thus, if: 1 maps to A, 2 maps to B, 3 maps to C, this function would be injective because each element of Set A has a distinct image in Set B.

Condition for Injectivity

For a function to be injective, it must satisfy the following condition −

• For any two elements a and b in Set A, if a ≠ b, then f(a) ≠ f(b) − This means that if two elements in Set A are different, their images in Set B must also be different.
• Number of elements in set A must be less than on equal to the number of elements in set B − This will also be injective.

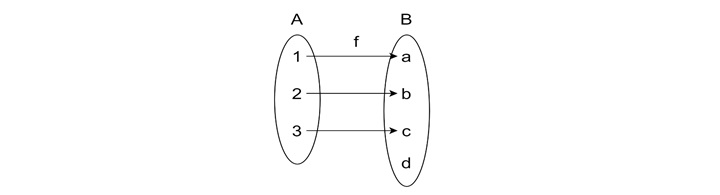
Number of Injective Functions

The number of possible injective functions depends on the sizes of Set A and Set B. Let's consider an example −

• Set A has 3 elements: {1, 2, 3}
• Set B has 4 elements: {A, B, C, D}

To find the total number of one-to-one functions from Set A to Set B, we use the formula for permutations −

• The first element in Set A has 4 possible choices in Set B.
• Once the first element is mapped, the second element has 3 choices.
• The third element then has 2 choices.

So, the total number of injective functions is: 4 × 3 × 2 = 24

This means there are 24 possible injective functions from Set A to Set B when Set A has 3 elements and Set B has 4 elements.

General Formula for Injective Functions

If Set A has m elements and Set B has n elements, the number of injective functions is given by −

$$\mathrm{n \: \times \: (n \:-\: 1) \: \times \: (n \:-\: 2) \: \times \: \dotso \: \times \: (n \:-\: m \:+\: 1)}$$

This is denoted as nPm, where P stands for permutations.

Special Case: When Sets A and B Are Equal

If the number of elements in Set A is equal to the number of elements in Set B (m = n), the formula simplifies to nPn, which is simply n! (n factorial).

Confusion with Many-to-One Functions

It is common to confuse one-to-one (injective) functions with many-to-one functions. In a many to one function, multiple elements in Set A can map to the same element in Set B. For example, if both 1 and 2 in Set A map to a in Set B, it is a many-to-one function.

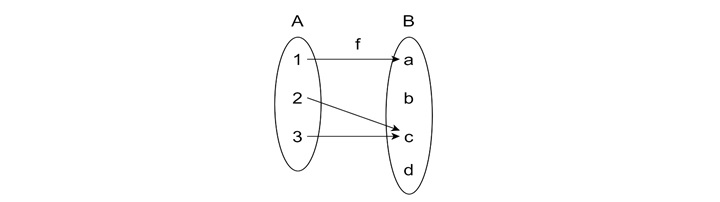
Not a Function

In the following example, there is a scenario where A has some element which is not mapped to B. This is not a function either, so there is no need to check one-to-one or anything else.

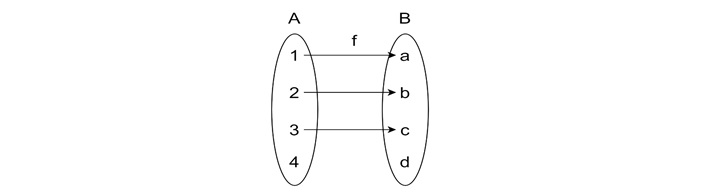
Real-World Applications of Injective Functions

Injective functions are not just theoretical; they have practical applications in computer science and other fields.

• Cryptography − In cryptography, injective functions are used in the design of encryption algorithms where each plaintext must map to a unique ciphertext to ensure secure communication.
• Database Management − In databases, injective functions help maintain data integrity by ensuring that unique keys map to unique records, preventing data duplication.

Conclusion

In this chapter, we covered one-to-one or injective functions, their definition, properties, and applications. We used examples to demonstrate what makes a function injective and explored the importance of injective functions in other real-world applications.