
- Time Series - Home
- Time Series - Introduction
- Time Series - Programming Languages
- Time Series - Python Libraries
- Data Processing & Visualization
- Time Series - Modeling
- Time Series - Parameter Calibration
- Time Series - Naive Methods
- Time Series - Auto Regression
- Time Series - Moving Average
- Time Series - ARIMA
- Time Series - Variations of ARIMA
- Time Series - Exponential Smoothing
- Time Series - Walk Forward Validation
- Time Series - Prophet Model
- Time Series - LSTM Model
- Time Series - Error Metrics
- Time Series - Applications
- Time Series - Further Scope
- Time Series Useful Resources
- Time Series - Quick Guide
- Time Series - Useful Resources
- Time Series - Discussion
Time Series - Moving Average
For a stationary time series, a moving average model sees the value of a variable at time t as a linear function of residual errors from q time steps preceding it. The residual error is calculated by comparing the value at the time t to moving average of the values preceding.
Mathematically it can be written as −
$$y_{t} = c\:+\:\epsilon_{t}\:+\:\theta_{1}\:\epsilon_{t-1}\:+\:\theta_{2}\:\epsilon_{t-2}\:+\:...+:\theta_{q}\:\epsilon_{t-q}\:$$
Whereq is the moving-average trend parameter
$\epsilon_{t}$ is white noise, and
$\epsilon_{t-1}, \epsilon_{t-2}...\epsilon_{t-q}$ are the error terms at previous time periods.
Value of q can be calibrated using various methods. One way of finding the apt value of q is plotting the partial auto-correlation plot.
A partial auto-correlation plot shows the relation of a variable with itself at prior time steps with indirect correlations removed, unlike auto-correlation plot which shows direct as well as indirect correlations, lets see how it looks like for temperature variable of our data.
Showing PACP
In [143]:
from statsmodels.graphics.tsaplots import plot_pacf plot_pacf(train, lags = 100) plt.show()
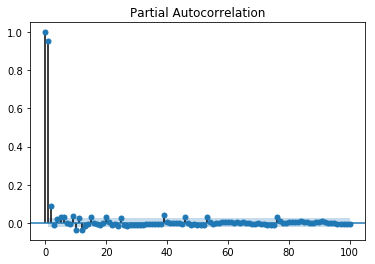
A partial auto-correlation is read in the same way as a correlogram.