Classes of Grammars in Compiler Design

Quiz

To perform syntax analysis in compiler design, we must focus on formal grammars. These grammars define the structure of a programming language through a set of formal rules that determine how valid sentences or code statements are constructed. However, not all formal grammars are the same.

Chomsky's hierarchy classifies grammars into four categories based on their complexity and expressive power. In this chapter, we will explore these grammar classes in the context of compiler design, breaking down each type with examples for better understanding.

What are Classes of Grammars?

Classes of grammars, are also known as Chomsky's hierarchy. They organize grammars into four levels −

Type 0: Unrestricted Grammars
Type 1: Context-Sensitive Grammars
Type 2: Context-Free Grammars
Type 3: Right-Linear Grammars

Here, each class is more restrictive than the one before. This means the Type 0 is less restricted than (Type 1, Type 2, Type 3). And when we go deeper they can generate fewer languages. However, they are also easier to implement and work with in compilers. Let us see them one by one.

Type 0: Unrestricted Grammars

Type 0 grammars have no restrictions at all on their production rules. They are the most general and powerful class of grammars.

Production Rules: The rules can be in any form like α → β

Here, α and β can be any string of terminal and nonterminal symbols. And as long as α is not empty, this is valid. For example,

Rule: SaB → cS

This rule is meaning that whenever the string SaB appears, it can be replaced with cS.

Application in Compiler Design − Type 0 grammars are not typically used in compilers because they are too general and computationally expensive. They describe languages that require Turing machines for parsing.

Type 1: Context-Sensitive Grammars

A little restricted grammar than Type0 is the Context-sensitive grammars or Type 1 grammar. They add restrictions to the rules. A nonterminal can only be replaced if it appears in a specific context.

Production Rules − The rules must follow this structure: αAγ → αβγ.

Here, A is a single nonterminal; α, β, and γ are strings of terminals and non-terminals; β cannot be empty.

It ensures that the replacement of A depends on the symbols around it (this is called the context). For example,

Rule: SaB − caB

Here we can say, S can only be replaced by c if it is followed by aB.

Application in Compiler Design − Context-sensitive grammars are powerful but we rarely see them in use of compilers design. This is because they are difficult to implement. They can describe languages like {aⁿbⁿcⁿ | n ≥ 0}, where the number of a’s, b’s, and c’s must match.

Type 2: Context-Free Grammars (CFGs)

Context-free grammars are the most commonly used in compiler design. They simplify rules by removing context dependence.

Production Rules: The rules are in the form: A → α, where A is a single non-terminal and α can be any string of terminals and non-terminals. For example,

Rule: S → aSb |

From this rule, it is clear that this is generating strings where a’s are followed by an equal number of b’s, like ab, aabb, or the null string ().

Application in Compiler Design: CFGs are widely used to define the syntax of programming languages. They are easy to parse and implement. Some examples include:

Arithmetic Expressions − E → E + T | T
Control Statements − S → if E then S else S

Type 3: Right-Linear Grammars

Next the mostly restricted grammar is the Right-linear grammars. They are mostly known as regular grammars. These grammars are the simplest. They are used to describe regular languages and are often used in lexical analysis.

Production Rules − Rules take one of these forms: A → aB, A → a, where A and B are non-terminals and a is a terminal. For example,

Rule: S → aA | b

It generates strings like ab, aaab, or just b.

Application in Compiler Design − The right-linear grammars are used to define tokens. For example keywords, identifiers, and constants in programming languages. They are used in tools like lexical analyzers. These tools rely on them for token recognition.

Relationships Among Grammar Classes

Chomsky's hierarchy can be visualized as nested circles:

Type 0 (Unrestricted) − The largest set of grammars
Type 1 (Context-Sensitive) − A subset of Type 0 grammars
Type 2 (Context-Free) − A subset of Type 1 grammars
Type 3 (Right-Linear) − A subset of Type 2 grammars

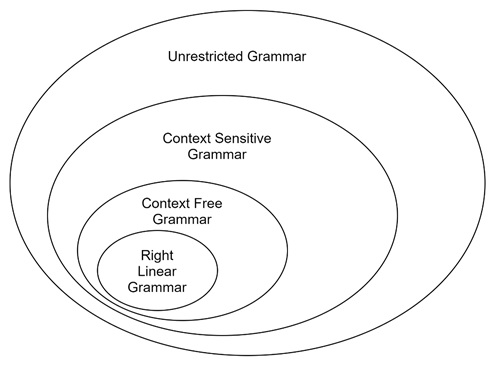
Every Type 3 grammar is also Type 2, Type 1, and Type 0. But, the reverse is not true. So not all Type 2 grammars are Type 3.

Examples of Grammars

Let us check out some examples of different types of grammars −

Palindromes Over {0, 1}

It's a Type 2 Context-Free Grammar (CFG).

G1:  
	S → 0S0  
	S → 1S1  
	S → 0  
	S → 1

This grammar generates palindrome strings like 000, 010, and 101.

Balanced Strings of a and b

It's a Type 2 Context-Free Grammar (CFG).

G2:  
	S → ASB  
	S →   
	A → a  
	B → b

This G2 grammar generates strings where the number of as equals the number of bs, such as "aabb" or "aaaabbbb".

Strings of as, bs, and cs

It's a Type 1 Context-Sensitive Grammar.

G3:  
	S → aSBC  
	S →   
	aB → ab  
	bB → bb  
	C → c

This grammar generates strings where the number of a’s equals the number of b’s and c’s. For example, "abc", "aabbcc", and "aaabbbccc".

Advantages of Grammar Classification

Following are the advantages of classifying the grammars into four different categories −

Clarity − Each class has well-defined rules. These rules are making it easier to choose the right type for a specific task.
Efficiency − Understanding the hierarchy will help in selecting the simplest grammar that meets the requirements.
Foundation for Parsing − Here each class corresponds to a different parsing strategy. This is such as regular expressions for Type 3 or pushdown automata for Type 2.

Challenges of Grammar Classes

The grammars also have certain limitations.

Complexity − Higher-level grammars (Type 0, Type 1) are powerful but hard to implement.
Ambiguity − Some grammars can generate the same string in multiple ways. This may complicating parsing process.
Practicality − Context-sensitive grammars are rarely used due to their computational overhead.

Conclusion

In this chapter, we explored the classes of grammars in compiler design, starting with Type 0 (unrestricted grammars) and progressing to Type 3 (right-linear grammars). We examined how each class defines different types of languages, from unrestricted and context-sensitive to context-free and regular languages.

Through examples such as palindromes and balanced strings, we demonstrated how these grammars are applied in real-world compiler tasks.

Print Page