
- Compiler Design - Home
- Compiler Design - Overview
- Compiler Design - Architecture
- Phases
- Compiler Design - Phases
- Compiler Design - Global Optimization
- Compiler Design - Local Optimization
- Lexical Analysis
- Compiler Design - Lexical Analysis
- Compiler Design - Regular Expressions
- Compiler Design - Finite Automata
- Compiler Design - Language Elements
- Compiler Design - Lexical Tokens
- Compiler Design - FSM
- Compiler Design - Lexical Table
- Compiler Design - Sequential Search
- Compiler Design - Binary Search Tree
- Compiler Design - Hash Table
- Syntax Analysis
- Compiler Design - Syntax Analysis
- Compiler Design - Parsing Types
- Compiler Design - Grammars
- Compiler Design - Classes Grammars
- Compiler Design - Pushdown Automata
- Compiler Design - Ambiguous Grammar
- Parsing
- Compiler Design - Top-Down Parser
- Compiler Design - Bottom-Up Parser
- Compiler Design - Simple Grammar
- Compiler Design - Quasi-Simple Grammar
- Compiler Design - LL(1) Grammar
- Error Recovery
- Compiler Design - Error Recovery
- Semantic Analysis
- Compiler Design - Semantic Analysis
- Compiler Design - Symbol Table
- Run Time
- Compiler Design - Run-time Environment
- Code Generation
- Compiler Design - Code Generation
- Converting Atoms to Instructions
- Compiler Design - Transfer of Control
- Compiler Design - Register Allocation
- Forward Transfer of Control
- Reverse Transfer of Control
- Code Optimization
- Compiler Design - Code Optimization
- Compiler Design - Intermediate Code
- Basic Blocks and DAGs
- Control Flow Graph
- Compiler Design - Peephole Optimization
- Implementing Translation Grammars
- Compiler Design - Attributed Grammars
Grammars in Compiler Design
When we write code, the compiler must determine whether it is a valid code or not. To identify that, the compiler depends on syntax analysis, which in turn relies on grammars.
Grammars, or formal grammars, define the rules that specify the syntax of a programming language. They dictate how individual elements, such as keywords and operators, combine to form valid statements and expressions. In this article, we will explore the concept of grammars, their structure, and their classification.
What are Grammars?
At a high level, a grammar is a formal system of set of rules. These rules are used to describe the structure of a language. These rules define which strings of symbols (or tokens) are valid within that language.
From our knowledge in formal languages, we know that the grammars are critical for programming languages because they show that written code follows a specific syntax.
Formally, we can say a grammar contains a set of parts.
- Terminal Symbols − The basic symbols that form the language. They are like letters, numbers, and operators (for example {0, 1}, {a, b}).
- Nonterminal Symbols − Symbols that represent groups of terminals or other non-terminals. They are often used to structure rules.
- Productions − Rules that describe how non-terminals can be replaced with terminals or other non-terminals.
- Starting Nonterminal − A specific nonterminal symbol from which derivations starts.
For example, in a programming language, terminal symbols could be any characters like +, -, a, b, or digits. Non-terminals might represent expressions, terms, or statements.
How Do Grammars Work?
Unlike natural language grammars, the formal language grammar generates strings in a language by starting with the starting nonterminal. This is repeatedly applying rules until only terminal symbols remain. This sequence of steps is called a derivation.
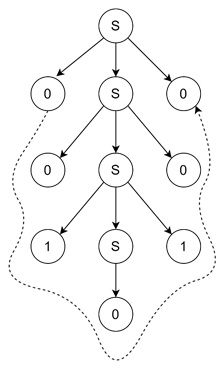
Just consider an example grammar, G1 −
G1: S → 0S0 S → 1S1 S → 0 S → 1
This grammar defines strings that are palindromes over the alphabet {0, 1}. Now we know a palindrome reads the same backward and forward.
Example of Derivation
Let us derive the string 0010100 using G1 −
Start with S (the starting nonterminal).
- Apply rule 1: S → 0S0 → 0S0
- Apply rule 1 again: 0S0 → 00S00
- Apply rule 2: 00S00 → 001S100
- Apply rule 3: 001S100 → 0010100
Thus, 0010100 is part of the language generated by G1.
Classification of Grammars
In 1959, Noam Chomsky introduced a classification system for grammars based on their complexity and expressive power. This system consists of four types of grammars: We will read the classification in more detail later but here is a basic overview.
Type 0: Unrestricted Grammars
Rules can have any string of terminals and non-terminals on either side of the production arrow. For example,
Rule: SaB → cS
These grammars can describe any computational problem that a Turing machine can solve.
Type 1: Context-Sensitive Grammars
The rules are of the form αAγ → αβγ, where A is a nonterminal and α, β, γ are strings of terminals and non-terminals. Here, the non-terminal A can only be replaced when it appears in the context of α and γ. For example,
Rule: SaB → caB
Type 2: Context-Free Grammars (CFGs)
Here the rules are of the form A → α, where A is a single nonterminal and α is any string of terminals and non-terminals. The CFGs are widely used in programming languages to define syntax. For example,
Rule: S → aSb
Type 3: Right-Linear Grammars
Here the rules are of the form A → aB or A → a, where A and B are non-terminals and a is a terminal. These grammars are used for lexical analysis by defining tokens like identifiers and constants.
Example of Grammars
Let us look at two grammars from the text −
Grammar G1: Palindromes
This grammar generates palindromes over {0, 1} −
G1: S → 0S0 S → 1S1 S → 0 S → 1
Language: {0, 1, 000, 010, 101, 111, 00000, }
Grammar G2: Balanced Strings of a and b
This grammar gives strings where the number of as equals the number of bs, and all as come before bs −
G2: S → ASB S → A → a B → b
Language: {, ab, aabb, aaabbb, …} = {anbn | n ≥ 0}
Derivation Example for aabb −
- Start with S
- Apply rule 1: S → ASB
- Apply rule 1 again: ASB → AASBB
- Apply rules 3 and 4: AASBB → AaBB → aabb
Context-Free Grammars in Programming Languages
In compiler design and syntax analysis, we generally use context-free grammars. In compiler design and syntax analysis, we generally use context-free grammars (CFGs). Most programming languages are defined using CFGs because they provide a balance between simplicity and expressive power.
CFGs are ideal for describing −
- Arithmetic expressions (E → E + T | T)
- Control structures (S → if E then S else S)
- Function definitions (F → def id(params) { S })
The rules for CFGs can also be written in the form called Backus-Naur Form (BNF). This is widely used notation in language design.
Advantages of Using Grammars
Following are the advantages of using grammars −
- Clarity − Grammars provide an easier and formal way to specify the syntax of a language.
- Error Detection − They help us the compilers to detect syntax errors during parsing.
- Automation − Tools like parser generators use grammars to automatically create syntax analyzers.
Challenges with Grammars
Like other concepts, grammars have limitations as well as advantages.
- Ambiguity − Some grammars can produce multiple derivation trees for the same string, leading to confusion.
- Complexity − Context-sensitive grammars are powerful but impractical for most compiler designs due to their complexity.
- Limitations − Certain aspects of programming languages, like semantic rules, cannot be captured by grammars alone.
Conclusion
In this chapter, we explored the concept of grammars and their significance in compiler design. We began by understanding what grammars are and how they generate strings in a language.
Through examples like G1 and G2, we saw how grammars define palindromes and balanced strings of "a" and "b". We also gained an overview of Chomsky's classification of grammars. Syntax analysis focuses on context-free grammars and their role in programming languages. Ultimately, we understood that grammars form the foundation of how programming languages are defined and interpreted.