Ambiguous Grammar in Compiler Design

---

---

In compiler design, the compilation process follows a series of phases to translate a program into a specific programming language. In syntax analysis, a critical goal is to ensure clarity, so the language avoids confusion for both developers and compilers. This is achieved by ensuring that each piece of code has only one possible interpretation. However, some grammars that define programming languages are inherently ambiguous, meaning a single string of code can generate multiple valid derivation trees, potentially leading to different interpretations.

Ambiguity in a language can result in compilation errors, inconsistent execution, or unnecessary complexity for developers. In this chapter, we will explore the concept of ambiguity in programming languages, examine its causes, and discuss various methods to resolve it, supported by examples for better understanding.

What is Ambiguity in Programming Languages?

In the context of compiler design, a grammar can be treated or considered as ambiguous if there exists at least one string of input that can generate multiple valid derivation trees. These derivation trees represent the syntactic structure of the input based on the rules defined by the grammars. If multiple trees can be generated, the meaning becomes unclear.

Consider the expression (var + var * var). Does the addition takes place first, or should multiplication take precedence? Since nothing is given there as additional input, compilers may interpret this differently. And this may be leading to unpredictable results.

Causes of Ambiguity

There are many such things which lead to make ambiguity in programming languages −

• Undefined Operator Precedence − When grammars do not specify the order in which operators should be evaluated, ambiguity may come.
• The Dangling Else Problem − Ambiguity in associating an else clause with one of several if statements.
• Multiple Derivation Paths − When a grammar allows multiple sequences of rule applications to produce the same string.

Example 1: Ambiguity in Arithmetic Expressions

Consider the grammar G1, which defines arithmetic expressions using addition and multiplication −

G1:  
	Expr → Expr + Expr  
	Expr → Expr * Expr  
	Expr → var  

This grammar is ambiguous. For the input (var + var * var), two derivation trees are possible −

Derivation Tree 1: Multiplication First

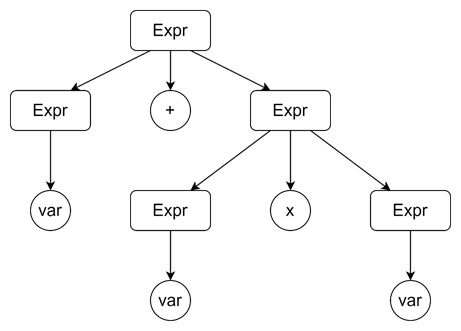
Derivation Tree 2: Addition First

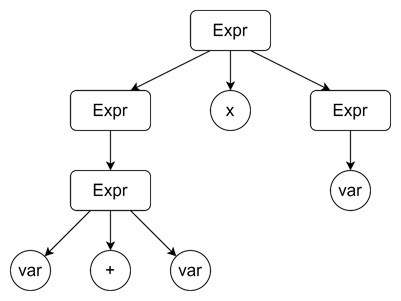
The two derivation trees represent different evaluation orders. And they are producing different results.

Resolving Ambiguity

To eliminate ambiguity, we can rewrite the grammar to enforce operator precedence. For example, multiplication should take precedence over addition. Here the revised grammar, G2, achieves this −

G2:  
	Expr → Expr + Term  
	Expr → Term  
	Term → Term * Factor  
	Term → Factor  
	Factor → ( Expr )  
	Factor → var  
	Factor → const  

Using G2, the input var + var * var has only one valid derivation tree −

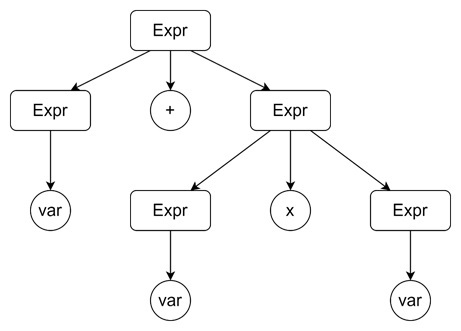
This tree ensures that multiplication occurs before addition, as expected.

Example 2: The Dangling Else Problem

Another classical ambiguity problem arises in conditional statements. Consider the following grammar G3 for if-else statements −

G3:  
	Stmt → IfStmt  
	IfStmt → if ( BoolExpr ) Stmt  
	IfStmt → if ( BoolExpr ) Stmt else Stmt  

For the input "if (Expr) if (Expr) Stmt else Stmt", two possible derivation trees exist −

Tree 1: The else Associates with the Closest if

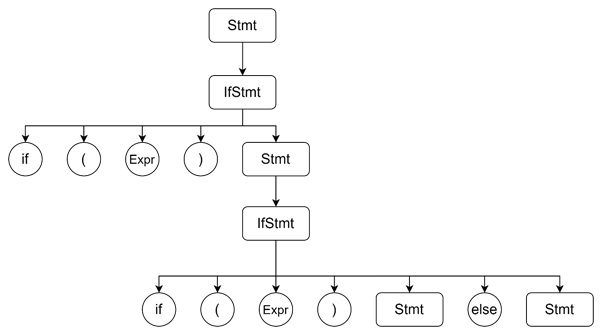
Tree 2: The else Associates with the Outer if

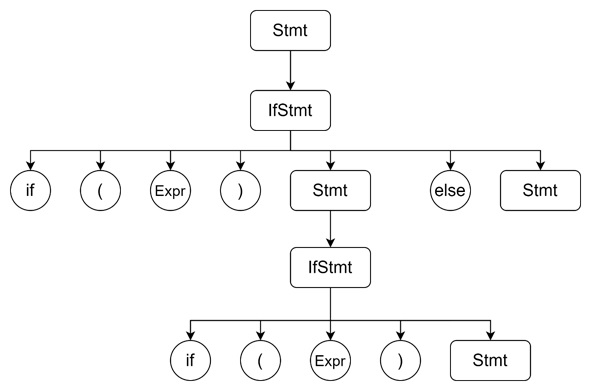
Resolving the Ambiguity

To resolve this ambiguity, we can rewrite the grammar to distinguish between if-else statements with and without a matching else. Now this revised grammar, G4, achieves this by introducing new nonterminals. This is for matched and unmatched if statements −

G4:  
	Stmt → IfStmt  
	IfStmt → Matched  
	IfStmt → Unmatched  
	Matched → if ( BoolExpr ) Matched else Matched  
	Matched → OtherStmt  
	Unmatched → if ( BoolExpr ) Stmt  
	Unmatched → if ( BoolExpr ) Matched else Unmatched  

Now, for the same input string, only one valid derivation tree exists. And this is ensuring that the else always associates with the closest unmatched if.

Effects of Ambiguity in Programming Languages

Ambiguity can lead to several problems −

• Compilation Errors − Ambiguous grammars make it harder for compilers to generate correct syntax trees.
• Inconsistent Behavior − Code may behave differently depending on the compiler.
• Developer Confusion − Ambiguity in syntax can make code harder to read and understand.

Strategies for Eliminating Ambiguity

Given below are some strategies for eliminating ambiguity −

• Rewriting Grammars − As seen in examples G2 and G4, rewriting grammars can resolve ambiguities. This can be done by enforcing precedence or associativity rules.
• Explicit Parentheses − Requiring parentheses in expressions avoids ambiguity. For example, (a + b) * c is unambiguous.
• Language Specifications − Clear rules, such as "an else always belongs to the nearest if," reduce confusion.

Real-World Applications

Ambiguity resolution is essential in real world applications. Such as −

• Arithmetic Parsing − Ensuring correct evaluation order for expressions in programming languages like Java or Python.
• Conditional Statements − Avoiding errors in nested if-else structures.
• Compiler Tools − Parser generators like YACC and ANTLR rely on unambiguous grammars for building syntax trees.

Conclusion

In this chapter, we explored the concept of ambiguity in programming languages and its impact on compiler design. Using examples such as arithmetic expressions and the "dangling else problem", we examined how ambiguous grammars can lead to multiple interpretations of the same input. We also discussed how rewriting grammars and enforcing precedence rules can resolve ambiguity.

In conclusion, while ambiguity poses a challenge in language design, it can be effectively addressed through careful planning and well-defined grammatical rules.