Cryptography - Feistel Block Cipher

A framework or design model called the Feistel cipher which is used to create different symmetric block ciphers, including DES. Components of this design framework can either be self-invertible, non-invertible, or invertible. The encryption and decryption algorithms are also the same as those used by the Feistel block cipher.

The Feistel structure demonstrates the implementation processes of confusion and diffusion and is based on the Shannon structure that was first described in 1945. Using a substitution method, confusion creates a complex relationship between the encryption key and the ciphertext. But diffusion uses a permutation process for creating a complex link between plaintext and cipher text.

The framework for implementing substitution and permutation alternately was proposed by the Feistel cipher. Substitution uses ciphertext to take the place of plaintext elements. Instead of having one element replace another as is done with substitution, permutation rearranges the elements of plaintext.

Algorithm

• Make a list of every character in plaintext.

• After converting the plaintext to ascii, format it in 8-bit binary.

• Separate the binary plaintext string into its left (L1) and right (R1) parts.

• For each of the two rounds, generate two random binary keys (K1 and K2), each of equal length to the plaintext.

Encryption

There are multiple rounds of processing plaintext in the Feistel cipher encryption process. The substitution step and the permutation step are included in every round. Take a look at the example that following, which describes the encryption structure used in this design framework.

• Step 1 − The plaintext is split up into fixed-size blocks, and only one block is handled at a time in this initial phase. Two inputs for the encryption technique are a block of plaintext and a key K.

• Step 2 − Split the block of plaintext into two parts. The plaintext block will have two distinct representations: LE0 for the left half of the block and RE0 for the right half. To create the ciphertext block, the two parts of the plaintext block (LE0 and RE0) will undergo multiple rounds of plaintext processing.

The encryption function is applied to the key Ki as well as the right half REi of the plaintext block for each round. Next, the left half of LEj is XORed with the function results. In cryptography, the logical operator XOR is used to compare two input bits and generate one output bit. For the following round, RE i+1, the output of the XOR function becomes the new right half. For the next round, the left half LEi+1 replaces the prior right half REi.

The same function, which implements a substitution function by applying the round function to the right half of the plaintext block, will be executed on each round. The left half of the block is used to XOR the function's output. After that, the two halves are switched using a permutation function. The next round's permutation results are given. Actually, the Feistel cipher model resembles the previously discussed Shannon structure in that it uses the substitution and permutation processes in an alternating manner.

Feistel Cipher Design Features

When using block ciphers, the following Feistel cipher design features are taken into account −

• Block size − Larger block sizes are considered to make block ciphers more secure. Larger block sizes, but it slow down how quickly the encryption and decryption processes execute. Block ciphers typically contain 64-bit blocks, while more recent versions, such as AES (Advanced Encryption Standard), have 128-bit blocks.

• Simple analysis − By making block ciphers simple to analyze, cryptanalytic vulnerabilities can be found and fixed, leading to the development of strong algorithms.

• Key size − Similar to block size, higher key sizes are considered to be more secure, but they can additionally cause the encryption and decryption process to take time to complete. The previous 64-bit key has been replaced by a 128−bit key in modern ciphers.

• The quantity of rounds − The quantity of rounds has an effect on a block cipher's security as well. More rounds boost security, but they also make the encryption harder to crack. The number of rounds therefore depends on the kind of data protection that a firm wants.

• Round function − An complex round function increases the security of the block cipher.

• Subkey generation function − Expert cryptanalysts find it more challenging to decrypt ciphers with more complex subkey generating functions.

• Fast software encryption and decryption − It is advantageous to use software that may boost block ciphers' rate of execution.

Decryption

The fact that the Feistel cipher model uses the same algorithm for both encryption and decryption may surprise you. A few important guidelines to keep in mind when decrypting are as follows −

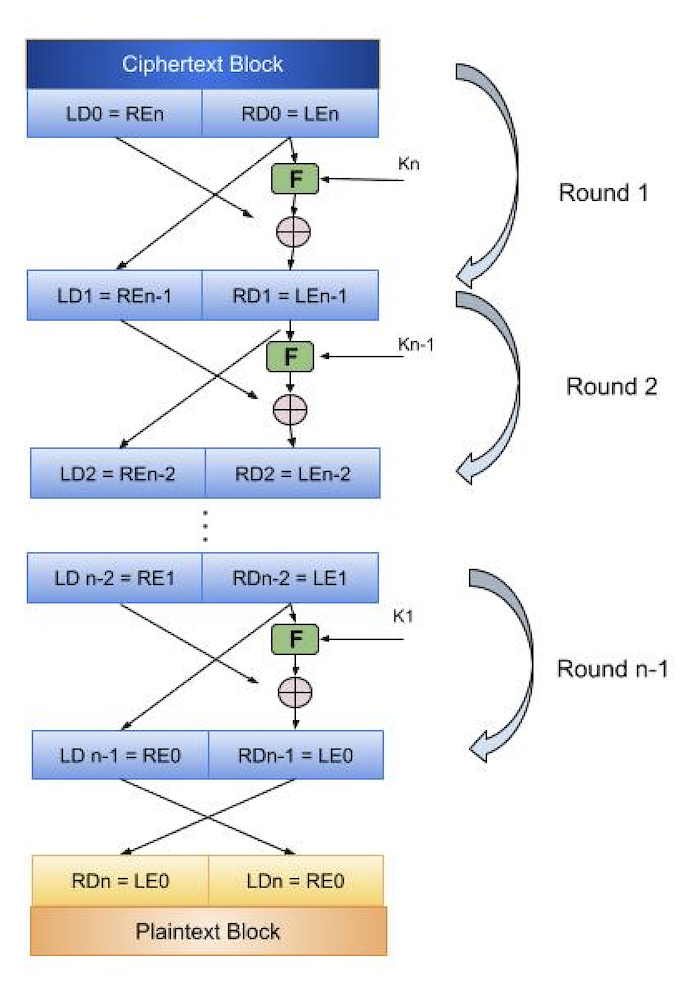
The encrypted text block is divided into two parts, the left (LD0) and the right (RD0), as seen in the above picture.

The round function is used with the key Kn-1 to operate on the right half of the cipher block, just like the encryption algorithm. The left half of the ciphertext block is XORed with the function's result. The output of the XOR function becomes the new right half (RD1), and RD0 swaps places with LD0 for the subsequent cycle. In fact, the identical function is used in each round, and the plaintext block is reached after a certain number of rounds are completed.

Implementation

The code implements the Feistel Block Cipher in Python, C, C++, and Java. It encrypts a plaintext string using two rounds of XOR operations with random keys and then decrypts it back to the original text.

The cipher splits the text into two halves, applies the XOR function with random keys, and swaps the halves.

Example

Following are the programs to implement the Feistel Block Cipher in C, C++, Java and Python −

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void random_key(int p, char *key) {
   for (int i = 0; i < p; i++) {
      key[i] = '0' + (rand() % 2);
   }
   key[p] = '\0';
}

void exor_func(char *a, char *b, char *result, int len) {
   for (int i = 0; i < len; i++) {
      result[i] = (a[i] == b[i]) ? '0' : '1';
   }
   result[len] = '\0';
}

int convert_bin_to_dec(char *binary) {
   int decimal = 0;
   for (int i = 0; binary[i] != '\0'; i++) {
      decimal = decimal * 2 + (binary[i] - '0');
   }
   return decimal;
}

int main() {
   char plaintext[] = "Hello Everyone";
   printf("Plain Text is: %s\n", plaintext);

   int len = strlen(plaintext);
   char plaintext_Bin[8 * len + 1];
   for (int i = 0; i < len; i++) {
      for (int j = 7; j >= 0; j--) {
         plaintext_Bin[8 * i + (7 - j)] = (plaintext[i] >> j) & 1 ? '1' : '0';
      }
   }
   plaintext_Bin[8 * len] = '\0';

   int n = len * 8 / 2;
   char L1[n + 1], R1[n + 1];
   strncpy(L1, plaintext_Bin, n);
   strncpy(R1, plaintext_Bin + n, n);
   L1[n] = '\0';
   R1[n] = '\0';

   int m = strlen(R1);
   char K1[m + 1], K2[m + 1];
   random_key(m, K1);
   random_key(m, K2);

   char f1[m + 1], R2[m + 1];
   exor_func(R1, K1, f1, m);
   exor_func(f1, L1, R2, m);
   char L2[m + 1];
   strncpy(L2, R1, m);
   L2[m] = '\0';

   char f2[m + 1], R3[m + 1];
   exor_func(R2, K2, f2, m);
   exor_func(f2, L2, R3, m);
   char L3[m + 1];
   strncpy(L3, R2, m);
   L3[m] = '\0';

   char bin_data[2 * m + 1];
   snprintf(bin_data, sizeof(bin_data), "%s%s", L3, R3);

   char str_data[8 * m + 1];
   int j = 0;
   for (int i = 0; i < 2 * m; i += 7) {
      char temp_data[8];
      strncpy(temp_data, bin_data + i, 7);
      temp_data[7] = '\0';
      int decimal_data = convert_bin_to_dec(temp_data);
      str_data[j++] = (char)decimal_data;
   }
   str_data[j] = '\0';

   printf("Cipher Text: %s\n", str_data);

   char L4[m + 1], R4[m + 1];
   strncpy(L4, L3, m);
   strncpy(R4, R3, m);

   char f3[m + 1], L5[m + 1];
   exor_func(L4, K2, f3, m);
   exor_func(R4, f3, L5, m);
   char R5[m + 1];
   strncpy(R5, L4, m);
   R5[m] = '\0';

   char f4[m + 1], L6[m + 1];
   exor_func(L5, K1, f4, m);
   exor_func(R5, f4, L6, m);
   char R6[m + 1];
   strncpy(R6, L5, m);
   R6[m] = '\0';

   char plaintext1[2 * m + 1];
   snprintf(plaintext1, sizeof(plaintext1), "%s%s", L6, R6);

   int num = strtol(plaintext1, NULL, 2);
   printf("Decrypted Plain Text is: %x\n", num);
   return 0;
}

Plain Text is: Hello Everyone
Cipher Text: A5BPYju	t{F_._..
Decrypted Plain Text is: ffffffff

#include <iostream>
#include <cstdlib>
#include <string>
#include <bitset>  // Added for safe binary to integer conversion

void random_key(int p, std::string &key) {
   for (int i = 0; i < p; i++) {
      key += '0' + (rand() % 2);
   }
}

void exor_func(const std::string &a, const std::string &b, std::string &result) {
   for (size_t i = 0; i < a.length(); i++) {
      result += (a[i] == b[i]) ? '0' : '1';
   }
}

int convert_bin_to_dec(const std::string &binary) {
   std::bitset<32> bits(binary);  // Safe conversion using bitset
   return static_cast<int>(bits.to_ulong());
}

int main() {
   std::string plaintext = "Hello Everyone";
   std::cout << "Plain Text is: " << plaintext << std::endl;

   std::string plaintextBin = "";
   for (char c : plaintext) {
      for (int i = 7; i >= 0; i--) {
         plaintextBin += (c >> i) & 1 ? '1' : '0';
      }
   }

   size_t n = plaintext.length() * 8 / 2;
   std::string L1 = plaintextBin.substr(0, n);
   std::string R1 = plaintextBin.substr(n);

   size_t m = R1.length();
   std::string K1, K2;
   random_key(m, K1);
   random_key(m, K2);

   std::string f1, R2;
   exor_func(R1, K1, f1);
   exor_func(f1, L1, R2);
   std::string L2 = R1;

   std::string f2, R3;
   exor_func(R2, K2, f2);
   exor_func(f2, L2, R3);
   std::string L3 = R2;

   std::string binData = L3 + R3;
   std::string strData = "";
   for (size_t i = 0; i < binData.length(); i += 7) {
      std::string tempData = binData.substr(i, 7);
      int decimalData = convert_bin_to_dec(tempData);
      strData += static_cast<char>(decimalData);
   }

   std::cout << "Cipher Text: " << strData << std::endl;

   std::string L4 = L3, R4 = R3;

   std::string f3, L5;
   exor_func(L4, K2, f3);
   exor_func(R4, f3, L5);
   std::string R5 = L4;

   std::string f4, L6;
   exor_func(L5, K1, f4);
   exor_func(R5, f4, L6);
   std::string R6 = L5;

   std::string plaintext1 = L6 + R6;

   int num = convert_bin_to_dec(plaintext1);
   std::cout << "Decrypted Plain Text is: " << std::hex << num << std::endl;

   return 0;
}

Plain Text is: Hello Everyone
Cipher Text: A5BPYju	t{F_._..
Decrypted Plain Text is: 48656c6c

import java.util.Random;
import java.math.BigInteger;

public class FeistelCipher {
   public static void randomKey(int p, StringBuilder key) {
      Random rand = new Random();
      for (int i = 0; i < p; i++) {
         key.append(rand.nextInt(2));
      }
   }

   public static void exorFunc(String a, String b, StringBuilder result) {
      for (int i = 0; i < a.length(); i++) {
         result.append(a.charAt(i) == b.charAt(i) ? '0' : '1');
      }
   }

   public static int convertBinToDec(String binary) {
      return Integer.parseInt(binary, 2);
   }

   public static void main(String[] args) {
      String plaintext = "Hello Everyone";
      System.out.println("Plain Text is: " + plaintext);

      StringBuilder plaintextBin = new StringBuilder();
      for (char c : plaintext.toCharArray()) {
         for (int i = 7; i >= 0; i--) {
            plaintextBin.append((c >> i) & 1);
         }
      }

      int n = plaintext.length() * 8 / 2;
      String L1 = plaintextBin.substring(0, n);
      String R1 = plaintextBin.substring(n);

      int m = R1.length();
      StringBuilder K1 = new StringBuilder(), K2 = new StringBuilder();
      randomKey(m, K1);
      randomKey(m, K2);

      StringBuilder f1 = new StringBuilder(), R2 = new StringBuilder();
      exorFunc(R1, K1.toString(), f1);
      exorFunc(f1.toString(), L1, R2);
      String L2 = R1.toString();  // Convert to String

      StringBuilder f2 = new StringBuilder(), R3 = new StringBuilder();
      exorFunc(R2.toString(), K2.toString(), f2);
      exorFunc(f2.toString(), L2, R3);
      String L3 = R2.toString();  // Convert to String

      String binData = L3 + R3;
      StringBuilder strData = new StringBuilder();
      for (int i = 0; i < binData.length(); i += 7) {
         String tempData = binData.substring(i, i + 7);
         int decimalData = convertBinToDec(tempData);
         strData.append((char) decimalData);
      }

      System.out.println("Cipher Text: " + strData);

      // Corrected line with explicit .toString()
      String L4 = L3.toString(), R4 = R3.toString();  // Use L3.toString() and R3.toString()

      StringBuilder f3 = new StringBuilder(), L5 = new StringBuilder();
      exorFunc(L4, K2.toString(), f3);
      exorFunc(R4, f3.toString(), L5);
      String R5 = L4;

      StringBuilder f4 = new StringBuilder(), L6 = new StringBuilder();
      exorFunc(L5.toString(), K1.toString(), f4);
      exorFunc(R5.toString(), f4.toString(), L6);
      String R6 = L5.toString();  // Convert to String

      String plaintext1 = L6 + R6;

      // Use BigInteger to handle large binary strings
      BigInteger num = new BigInteger(plaintext1, 2);
      System.out.println("Decrypted Plain Text is: " + num.toString(16));
   }
}

Plain Text is: Hello Everyone
Cipher Text: OI;-o.Gj.H/%j{p,
Decrypted Plain Text is: 48656c6c6f2045766572796f6e65

import binascii
import random

def random_key(p):
   key = ""
   p = int(p)
   for _ in range(p):
      temp = random.randint(0, 1)
      temp = str(temp)
      key = key + temp
   return key

def exor_func(a, b):
   temp = ""
   for i in range(len(a)):
      if a[i] == b[i]:
         temp += "0"
      else:
         temp += "1"
   return temp

def convert_bin_to_dec(binary):
   string = int(binary, 2)
   return string

plaintext = "Hello Everyone"
print("Plain Text is:", plaintext)

plaintext_Ascii = [ord(x) for x in plaintext]
plaintext_Bin = [format(y, '08b') for y in plaintext_Ascii]
plaintext_Bin = "".join(plaintext_Bin)

n = len(plaintext_Bin) // 2
L1 = plaintext_Bin[0:n]
R1 = plaintext_Bin[n::]
m = len(R1)

K1 = random_key(m)
K2 = random_key(m)

f1 = exor_func(R1, K1)
R2 = exor_func(f1, L1)
L2 = R1

f2 = exor_func(R2, K2)
R3 = exor_func(f2, L2)
L3 = R2

bin_data = L3 + R3
str_data = ''

for i in range(0, len(bin_data), 7):
   temp_data = bin_data[i:i + 7]
   decimal_data = convert_bin_to_dec(temp_data)
   str_data = str_data + chr(decimal_data)

print("Cipher Text:", str_data)

L4 = L3
R4 = R3

f3 = exor_func(L4, K2)
L5 = exor_func(R4, f3)
R5 = L4

f4 = exor_func(L5, K1)
L6 = exor_func(R5, f4)
R6 = L5
plaintext1 = L6 + R6

plaintext1 = int(plaintext1, 2)
Rplaintext = binascii.unhexlify('%x' % plaintext1)
print("Decrypted Plain Text is: ", Rplaintext)

Plain Text is: Hello Everyone
Cipher Text: 
9.&ab.Hty}QY.]M
Decrypted Plain Text is:  b'Hello Everyone'

Summary

Organizations can use the popular encryption design concept known as the Feistel cipher to help secure their sensitive data. A robust encryption cipher should keep a hacker from deciphering the cipher plain text without the key or sets of keys, even if they are aware of the cipher algorithm.

Businesses should implement a layered cyber-security approach in addition to this cipher model to help stop attackers from stealing or disclosing their confidential data.