Binomial Coefficients in Discrete Mathematics

---

---

Binomial coefficients are used not only in combinatorics, but also in probability and algebra. They are useful in counting, especially when we are choosing elements from a set without considering the order. Binomial coefficients are nothing but the expansion of binomials. They are expressions of the form $\mathrm{(x + y)^n}$. Every time we multiply out a binomial like this, the binomial coefficients are useful in figure out the size of the terms in the expansion.

Read this chapter to learn what binomial coefficients are and how to calculate them.

What are Binomial Coefficients?

As we know, a binomial coefficient is written using a notation that looks like this −

$$\mathrm{\binom{n}{k}}$$

This is read as "n choose k" and represents the number of ways to choose k elements from a set of n elements. Here we do not have to care about the order. For instance, if we want to know how many ways there are to choose 2 items out of 5 (like we are picking 2 apples from a basket of 5 different apples), we would use the binomial coefficient .

$$\mathrm{\binom{5}{2}}$$

The formula for calculating binomial coefficients is −

$$\mathrm{\binom{n}{k} \:=\: \frac{n!}{k!(n\:-\:k)!}}$$

The n! means "n factorial," which is the product of all positive integers from 1 up to n. For example,

$$\mathrm{5! \:=\: 5\: \times\: 4\: \times\: 3\: \times\: 2\: \times\: 1 \:=\: 120}$$

Example of Calculating a Binomial Coefficient

Let us work through an example. If we wanted to know how many ways we can select 3 objects out of 5, we would calculate $\mathrm{\binom{5}{3}}$.

$$\mathrm{\binom{5}{3} \:=\: \frac{5!}{3!(5\:-\:3)!} \:=\: \frac{5 \:\times\: 4 \:\times\: 3!}{3!2!} \:=\: \frac{5 \:\times\: 4}{2!} \:=\: 10}$$

So, there are 10 ways to choose 3 objects from a group of 5.

Binomial Expansions

Now that we understood how to calculate binomial coefficients, let us go through how they fit into the expansion of binomials. Suppose we want to expand the expression $\mathrm{(x \:+\: y)^n}$. The binomial coefficients will tell us the coefficients of the terms in the expanded version of this expression.

For example, when we expand $\mathrm{(x \:+\: y)^3}$, we get −

$$\mathrm{(x \:+\: y)^3 \:=\: x^3 \:+\: 3x^2y \:+\: 3xy^2 \:+\: y^3}$$

See, the numbers in front of the terms: 1, 3, 3, and 1. These are binomial coefficients! They tell us how many times each combination of x and y appears in the expansion. In this case, the coefficients come from $\mathrm{\binom{3}{0},\: \binom{3}{1},\: \binom{3}{2}}$ and $\mathrm{\binom{3}{3}}$.

Expanding Larger Binomials

Let us expand $\mathrm{(x \:+\: y)^5}$. Using the binomial coefficients, we can expand it like −

$$\mathrm{(x \:+ \:y)^5 \:=\: x^5 \:+\: 5x^4y \:+\: 10x^3y^2 \:+\: 10x^2y^3 \:+\: 5xy^4 \:+\: y^5}$$

Again, the binomial coefficients here are $\mathrm{\binom{5}{0} \:=\: 1,\: \binom{5}{1} \:=\: 5,\: \binom{5}{2} \:=\: 10,\: \binom{5}{3} \:=\: 10,\: \binom{5}{4} \:=\: 5}$ and $\mathrm{\binom{5}{5} \:=\: 1}$ These coefficients help us to expand the binomial quickly and correctly.

Binomial Coefficients and Counting Problems

Binomial coefficients are also useful in counting problems. When we find out how to choose things from a group, we are likely using binomial coefficients, even if we do not realize it. Let us see this claim through examples.

Example 1: Choosing a Subset

Consider we have a set of five elements, say {1, 2, 3, 4, 5} and we want to know how many ways we can select three elements from that set. This is exactly the same problem as asking for $\mathrm{\binom{5}{3}} $, which, as we calculated earlier, is 10. So, there are 10 ways to pick a subset of three elements from a set of five.

Example 2: Forming Committees

Here is another example where we are organizing a committee and need to pick 2 members from a group of 6 people. The number of ways we can do this is $\mathrm{\binom{6}{2}}$, which is calculated as −

$$\mathrm{\binom{6}{2} \:=\: \frac{6!}{2!(6\:-\:2)!} \:=\: \frac{6 \:\times\: 5 \:\times\: 4!}{2!4!} \:=\: \frac{30}{2!} \:=\: 15} $$

So, there are 15 different ways to form this 2-person committee from the 6 people.

Recurrence Relation for Binomial Coefficients

Other aspect for binomial coefficients are they follow a recurrence relation. This means that we can calculate any binomial coefficient based on smaller binomial coefficients. Specifically, the relation is −

$$\mathrm{\binom{n}{k} \:=\: \binom{n\:-\:1}{k\:-\:1} \:+\: \binom{n\:-\:1}{k}}$$

What this says is that to calculate $\mathrm{\binom{n}{k}}$, we can add up two smaller coefficients: $\mathrm{\binom{n\:-\:1}{k\:-\:1}}$ and $\mathrm{\binom{n\:-\:1}{k}}$. This relationship is useful because it lets us build up larger binomial coefficients from smaller ones.

Example of Recurrence Relation

Let us see some example. Say we want to calculate $\mathrm{\binom{5}{3}}$, but we do not want to use the factorial formula. Instead, we can break it down using the recurrence relation −

$$\mathrm{\binom{5}{3} \:=\: \binom{4}{2} \:+\: \binom{4}{3}}$$

We know from earlier that $\mathrm{\binom{4}{2}}$ is 6 and $\mathrm{\binom{4}{3}}$ is 4, so

$$\mathrm{\binom{5}{3} \:=\: 6 \:+ \:4 \:=\: 10}$$

We get the same result as before, but by using smaller pieces to build up the solution.

Pascals Triangle

Another way to visualize binomial coefficients is through the Pascals Triangle. The Pascals Triangle is a triangular arrangement of binomial coefficients, where each number is the sum of the two numbers directly above it.

Here is a small version of Pascals Triangle −

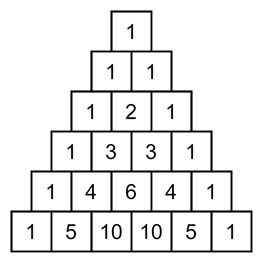
Each row corresponds to the binomial coefficients for a particular power of a binomial expansion. The top row (1) corresponds to $\mathrm{(x \:+\: y)^0}$, the next row (1, 1) corresponds to $\mathrm{(x \:+\: y)^1}$, and so on.

We can use Pascals Triangle to quickly find binomial coefficients. For example, to find $\mathrm{\binom{5}{3}}$, just look in the sixth row (because it corresponds to $\mathrm{(x \:+\: y)^5}$ and find the fourth number, which is 10.

Conclusion

In this chapter, we explored what binomial coefficients are and how they are used in discrete mathematics. We explained their role in expanding binomials and how to calculate them using both factorials and Pascals Triangle. We also understood the recurrence relation that binomial coefficients follow, which makes them easy to calculate step by step.

In the next chapter, we will discuss the Pascals triangle in more detail with its applications and where we could use them.