Properties of Trees in Discrete Mathematics

---

---

Trees are special types of graphs. Unlike other types of graphs, trees have some unique properties. A tree is a connected graph with no cycles. It is a simple yet powerful structure that finds its applications across many fields such as data organization, algorithms, network design, and biology.

In this chapter, we will cover some key properties of trees and understand their definitions and propositions with the help of examples.

Trees in Graph Theory

Trees are a special form of graph in which all vertices are connected, but there are no cycles. It means, any path from one vertex to another will be unique and will not loop back to any previous point. For n number of vertices, it must have n – 1 number of edges to form a connected graph as a tree.

Formally, a tree is defined as a connected acyclic graph. If the tree is not connected, it is referred to as a forest. Forest is nothing but a group of unconnected acyclic graphs.

Trees provide a clear path between vertices, and make them helpful in cases where a hierarchical structure is required, such as decision-making processes or family trees.

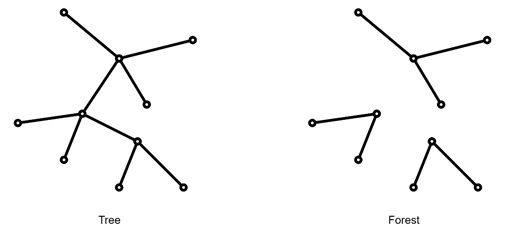
Basic Properties of Trees

Let us see some of the basic properties of trees that make them special and useful in various applications. Here, we will highlight the properties related to connectivity, uniqueness of paths, and the relationship between vertices and edges.

Connectivity and Acyclic Nature

As we know, by definition, a tree is connected, it means there is a path between any pair of vertices. At the same time, it is acyclic, so it contains no loops or cycles. This combination of properties ensures that if there is a path between two vertices, that path will be unique.

Example

Imagine we have a family tree where each person has a unique connection to their ancestors and descendants. If we create paths to represent family relations, no loops will form, and only one direct connection from a child to a parent without any chance of repeating the connection.

Since a tree with n vertices will be connected, then there it can be proved that if we have n-2 vertices all nodes will not be connected. And, if we have n edges, there will be an edge which is parallel or forming a cycle. So, a tree must have n - 1 edges.

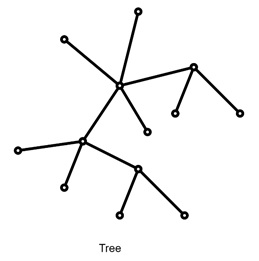
Here, we have 13 nodes and 12 edges.

Key Propositions about Trees

Propositions in graph theory gives the mathematical explanations for why certain properties hold. Let us see some crucial propositions that help define trees and illustrate why they behave differently from other graphs.

Unique Path Proposition

The unique path property is special in distinguishing trees from other graphs. Let us see the technique to prove this −

Proof Outline

To prove that a tree has a unique path between any two vertices, we assume that there is more than one path between two points. And this assumption makes it to a contradiction because it would imply the presence of a cycle. This is against the definition of a tree. So, we confirm the uniqueness of the path in a tree.

Leaves in Trees

Leaves in a tree are vertices that have only one edge connecting them to another vertex. This means their degree is one. Trees with multiple vertices always have at least two leaves.

Proposition

Any tree with at least two vertices has at least two vertices of degree one (leaves). This characteristic is special and used in various algorithms to simplify tree structures. By reducing a tree to smaller sub-trees that maintain the tree's properties.

Here, the boxes are leaves and round nodes are non-leaves. All boxes are of degree 1.

Example

Consider a tree representing a simple binary hierarchy in an organization. If the CEO is at the top, the entry-level employees are at the leaves, each reporting to only one manager or department head. So this ensures that each leaf, or endpoint, has a degree of one.

Relationship between Vertices and Edges

We have already talked about for v number of vertices we have v – 1 number of edges. Let prove this with induction −

Proof by Induction

Consider from a tree with one vertex (no edges) and building up by adding vertices and edges while maintaining the structure of a tree.

• Base Case − A tree with a single vertex has zero edges.
• Inductive Step − For a tree with k vertices, adding another vertex and connecting it with an edge preserves the tree structure, which will make k + 1 vertices and k edges.

This property shows for v – 1 edges for v vertices is needed for graph validation. This is especially in spanning trees and minimum spanning trees.

Applications of Trees in Spanning Graphs

Trees are useful in creating subgraphs called spanning trees. A spanning tree is a subset of a connected graph that gives all vertices but has only enough edges to form a tree. Spanning trees are used in various algorithms like network design and optimization.

Example of Spanning Tree

Consider we need to make an electrical wires in a building. We want to connect all rooms (vertices) with the least amount of wiring (edges) without any redundant loops. A spanning tree provides a solution, and connecting all vertices while minimizing the number of edges.

Finding a Spanning Tree

There are multiple ways to find a spanning tree within a graph. For example −

Cycle Removal

Start with the graph and remove edges until no cycles remain. It will then be a graph with connected nodes and no cycles.

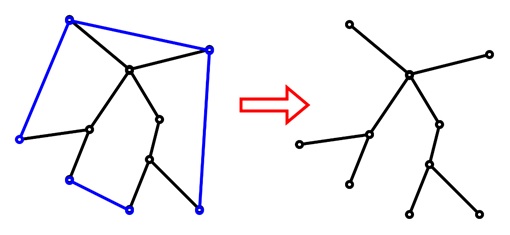
See we are removing the blue edges from the graph to form a spanning tree.

Edge Addition

Start with an empty graph, adding edges until all vertices are connected without forming cycles.

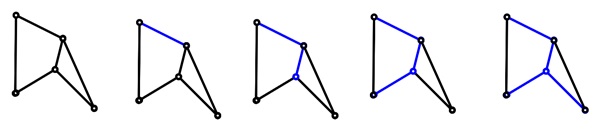
From the graph we are adding edges (in blue) and it is forming a spanning tree.

Real-World Analogies of Trees

To better understand trees, let us see some real-world examples and analogies −

• Family Trees − Family trees are practical examples, where each node represents a family member, and edges represent relationships. The structure gives no cycles since no individual can be their own ancestor or descendant.
• Organizational Hierarchies − Many companies use a hierarchical, tree-like structure where each department or employee reports to a single manager. This layout avoids cycles, ensuring clear, direct paths of accountability and reporting.

Conclusion

Trees are defined as connected, acyclic graphs that has distinct properties like the unique path property and a specific relationship between vertices and edges.

In this chapter, we explained the basic properties and the unique characteristics of trees in discrete mathematics. We have also understood the importance of leaves in trees, their application in spanning graphs, and real-world applications.