Non-Planar Graphs in Discrete Mathematics

---

---

Non-planar graphs in graph theory are special type of graphs that cannot be drawn on a paper without intersecting the edges. Planar graphs can be drawn on a plane while non-planar graphs are the exact opposite of them. These graphs offer an insight into the practical and theoretical aspects of graph theory.

In this chapter, we will cover the basics of non-planar graphs, check some famous examples, and understand the proofs and reasoning behind non-planarity.

What is a Non-Planar Graph?

A non-planar graph is a graph that cannot be drawn on a plane without at least some of its edges crossing. In a planar graph, we can always find a way to redraw it. It may be complex but there is a way. But in a non-planar graph, this is simply impossible.

Take a look at the following example −

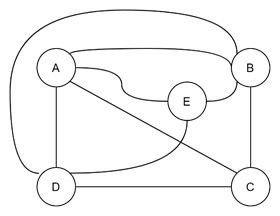
Recognizing Non-Planar Graphs

To recognize a non-planar graph, we usually apply two key approaches −

• Redrawing Attempts − By trying to arrange the graph in various ways and seeing if we can avoid edge crossings. If we fail, the graph is likely non-planar. But this method is taking exhaustive searching. So the next theorem based method comes.
• Applying Theorems − There are some theorems, like Kuratowski’s theorem. It provides conditions that let us determine non-planarity without redrawing.

Non-planar graphs are not only a theoretical concept. They appear in real-world problems like designing circuits, where pathways cannot overlap, or in networks where certain connections must remain separate. Understanding non-planar graphs helps to understand these problems and avoid potential "crossing conflicts."

Classic Examples of Non-Planar Graphs

There are two famous examples of non-planar graphs −

• The complete graph K₅
• The complete bipartite graph K_3,3

These graphs not only illustrate the concept of non-planarity but also show the mathematical methods used to prove non-planarity.

The Complete Graph K₅

The complete graph K₅ includes five vertices. Here each connected to every other vertex. They are resulting in ten edges. They can be called as "complete" because it contains all possible edges between the vertices. It makes K₅ non-planar −

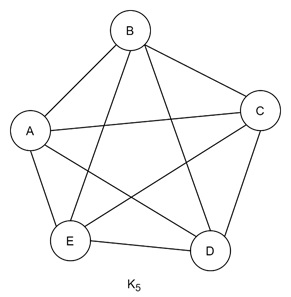
If we try drawing K5 on paper, we will notice that some edges have to cross. No matter how we arrange the vertices or redraw the edges, at least one edge will always overlap another. But this claim can also be proven formally.

Proof of Non-Planarity in K₅

To prove K₅ is non-planar, we assume for a moment that it could be planar. If K₅ were planar, it would satisfy Euler’s formula for planar graphs, which states −

$$\mathrm{v \:-\: e \:+\: f \:=\: 2}$$

where −

• v is the number of vertices,
• e is the number of edges,
• f is the number of faces.

For K₅, we have: v = 5 and e = 10.

Plugging these into Euler's formula, we get −

$$\mathrm{5 \:-\: 10 \:+\: f \:=\: 2 \:\Rightarrow\: f \:=\: 7}$$

This means that if K5 were planar, it would have seven faces. But, another condition of planar graphs states that the total number of edges around all faces (it that is B), then it must meet certain requirements −

• Each face needs at least three edges around it, so B ≥ 3f
• Since each edge borders two faces, B = 2e.

Given that e = 10, we find B = 2 × 10 = 20.

To satisfy B ≥ 3f, we need −

$$\mathrm{20 \:\geq\: 3 \:\times\: 7 \:=\: 21}$$

This inequality doesn't hold. So it proves that K₅ cannot be planar.

The Complete Bipartite Graph K_3,3

Another classic example of a non-planar graph is the complete bipartite graph K_3,3. This graph has two sets of vertices, each with three vertices. Every vertex in one set connects to every vertex in the other set, forming a bipartite structure.

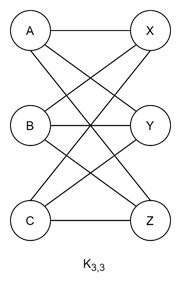
In real life, K_3,3 can be visualized as the "three houses and three utilities problem," where three houses need connections to three utilities without any lines crossing. It may look simple in words, but we cannot get it done because it is impossible to solve without crossings!

Proof of Non-Planarity in K_3,3

The proof for K_3,3 is similar to that of K₅. We are using again on Euler’s formula and boundary conditions:

Assume Planarity − Suppose K_3,3 could be drawn without any edges crossing.

Apply Euler's Formula − For K_3,3, we have −

• v = 6,
• e = 9.

Using Euler's formula, we calculate −

$$\mathrm{6 \:-\: 9 \:+\: f \:=\: 2 \:\Rightarrow\: f \:=\: 5}$$

So, if K_3,3 were planar, it would have five faces.

Boundaries Around Faces: Each face in K_3,3 needs at least four edges (as there are no three-edge cycles in bipartite graphs), we set up the condition −

• B ≥ 4f
• B = 2e

With e = 9, B = 2 × 9 = 18. For B ≥ 4f, we get −

$$\mathrm{18 \:\geq\: 4 \:\times\: 5 \:=\: 20}$$

This inequality fails, and it proves that K_3,3 cannot be planar.

Comparing K₅ and K_3,3

While both K₅ and K_3,3 are non-planar, their structures are different. K₅ is a complete graph where every vertex connects to every other vertex, creating dense connections.

In contrast, K_3,3 is a complete bipartite graph, dividing vertices into two groups where each vertex in one group connects to each vertex in the other group. These differences makes the various types of complexity which lead to non-planarity.

Applications of Non-Planar Graphs

Non-planar graphs have several practical applications in fields where we need to draw elaborate layouts, some of which are listed below −

• Circuit Design − In designing circuits on a chip, we aim to place wires without intersections to avoid interference. So recognizing non-planar layouts helps to prevent design errors and makes circuits more efficient.
• Network Routing − Non-planar graphs can also be used to model complex networks like transportation grids or communication systems, where certain routes should avoid crossing paths to maintain efficiency and reduce congestion.
• 3D Modeling and Geometry − For 3D modelling non-planar concepts apply to three-dimensional polyhedra and spatial structures. These are used in understanding of polyhedral properties and projections.

Conclusion

In this chapter, we covered the basics of non-planar graphs. We checked the classic examples like K₅ and K_3,3, and understood the proofs showing their non-planarity.

We saw that non-planar graphs cannot be drawn on a plane without crossing edges. With Euler's formula and boundary conditions, we understood why certain graphs fail to be planar.