Planar Graphs in Discrete Mathematics

---

---

Graph theory is a part of discrete mathematics, where we see different types of graphs in action. Planar graphs are a special type of graph. They are special because they can be drawn in a two dimensional plane without any edges crossing.

In this chapter, we will see the basics of planar graphs with easy-to-understand examples along with the explanations of core concepts like Eulers formula and non-planar graphs.

What is a Planar Graph?

A planar graph is a special type of graph that can be drawn on a flat plane. No two edges intersect except at their endpoints (vertices). When a graph is drawn this way, it divides the plane into distinct regions known as faces.

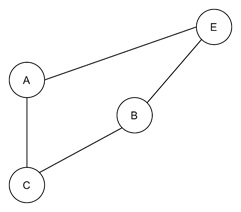
Here we have 4 vertices and they have no intersecting edges so it is a planer graph.

Drawing Planar Graphs

For a graph to be planar, we must draw it in a way that it prevents edges from crossing each other. So, sometimes a graph may look non-planar initially, but with careful redrawing, it can be made planar.

Let us understand this concept with a simple example. Take a look at the following graph.

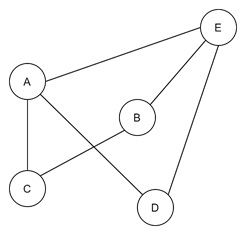
It is a graph with 5 vertices and 6 edges. It is not a planar graph because it has two edges AD and BC which are intersecting each other.

Let's now draw the same graph in a different way; like the one shown below −

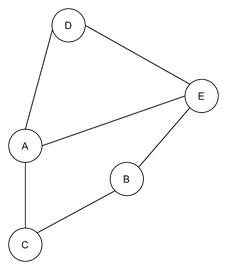
Observe that it is the same graph but its vertex D is now placed outside and it has now transformed into a planer graph.

Let us now take a look at a non-planar graph −

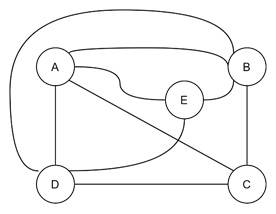
Wherever we might try to place the vertex E, it will never become a planar graph.

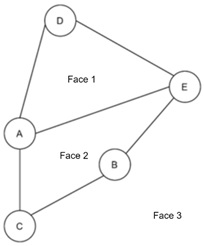
Faces in Planar Graphs

A planar graph can be successfully drawn without any crossing edges. The edges and vertices naturally split the plane into regions, or faces. As we know, one of these regions will always be the "outside" of the graph, forming a boundary that encircles everything else.

Eulers Formula: A Key Concept in Planar Graphs

When we are talking about planar graphs, we must follow the Eulers formula. This is much useful to relate the vertices, edges, and faces of any connected planar graph.

For any planar graph, the Eulers formula states −

$$\mathrm{v \:-\: e \:+\: f \:=\: 2}$$

where −

• v is the number of vertices,
• e is the number of edges,
• f is the number of faces.

Applying Eulers Formula

Consider the previous example with faces. We have 5 vertices, 6 edges and 3 faces. If we plug them into the formula, it will become −

$$\mathrm{5 \:-\: 6 \:+\: 3 \:=\: 2}$$

This verifies that Eulers formula holds. For any connected planar graph, whether simple or complex, the values of vertices, edges, and faces will satisfy this equation.

The Eulers formula is true regardless of the arrangement of vertices or edges for a connected planar graph. Even if we add extra vertices and edges, as long as the graph can be redrawn without any edge intersections, it will continue to satisfy the Eulers formula.

What are Non-Planar Graphs?

If a graph cannot be drawn on a plane, it belongs to the category of non-planar graphs. When there are too many edges for the number of vertices, it becomes impossible to draw the graph without intersecting edges.

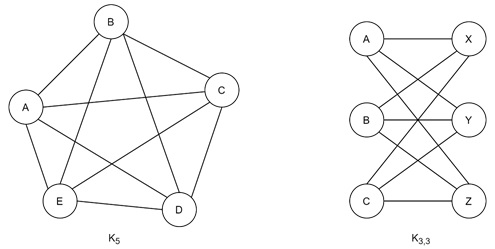
A complex example like complete graphs K₅ (with 5 vertices) and the complete bipartite graph K_3,3 are classic examples of non-planar graphs.

Example of Non-Planar Graphs

The graph K₅ has 5 vertices connected to every other vertex. It has 10 edges. Euler's formula and additional conditions for planarity show that K₅ cannot be drawn without edges crossing. Similarly, the bipartite graph K_3,3 consists of two sets of three vertices.

Every vertex from one set is connected to every vertex in the other. This setup is mathematically impossible to achieve on a plane without intersections.

Applications of Planar Graphs: Polyhedra and Beyond

Planar graphs have a large variety of applications, particularly in geometry. For instance, they can be used to represent polyhedral. This is a three-dimensional solids with flat faces and straight edges.

When a polyhedron like a cube is projected onto a plane, it forms a planar graph. Here the vertices and edges of a cube satisfy Eulers formula. It has eight vertices, twelve edges, and six faces. We will see Polyhedra in detail in the next chapter.

Regular Polyhedra: The Five Platonic Solids

The concept of polyhedra using planar graphs can be extended to the five regular polyhedral. They are also known as the Platonic solids. These solids are special because each face is an identical polygon. Every vertex connects the same number of edges.

The five regular polyhedra are −

• Tetrahedron
• Cube
• Octahedron
• Dodecahedron
• Icosahedron

Theorems and Proofs in Planar Graph Theory

Let us see some special proofs based on planar graphs.

Proving Non-Planarity: A Look at K₅ and K_3,3

Proofs for the non-planarity of graphs like K₅ and K_3,3 often rely on logical contradiction. We may think of that the graph is planar, we can apply Euler’s formula, and find that certain required conditions cannot be met.

For instance, with K₅, if we assume planarity, we find that the number of edges surrounding the faces creates an impossible situation. This is proving that no planar representation exists.

Girth and Boundaries in Planar Graphs

In more complex cases, the concept of girth (the length of the shortest cycle in a graph) helps determine whether a graph is planar. By analyzing the boundaries surrounding the faces, one can establish whether a planar arrangement is impossible. If specific girth and boundary conditions are not met, the graph cannot be planar.

Conclusion

In this chapter, we explained the concept of planar graphs. Starting with the basic definition and moving through fundamental concepts such as faces, we covered the Euler's formula and its applications in geometry. We also touched upon non-planar graphs to provide a clear understanding of why certain graphs cannot avoid edge intersections.

We covered how planar graphs relate to polyhedra and discovered how the properties of regular polyhedra like the Platonic solids reflect the principles of planar graph theory.