Coloring Edges in Discrete Mathematics

---

---

When we talk about graph coloring, generally we focus on vertex coloring. Coloring the edges is equally important in discrete mathematics.

In this chapter, we will explain the fundamentals of edge coloring concept. We will see how edge coloring can be used in various applications and why it is useful and challenging to determine the minimum number of colors required.

Basics of Edge Coloring

Edge coloring is used to assign colors to the edges of a graph. The goal is to make sure that no two edges that share a vertex (adjacent edges) are given the same color. This is called the proper edge coloring.

There is another concept called the chromatic index. It is denoted as χ′(G). The chromatic index gives the minimum number of colors required to achieve a proper edge coloring of a graph G. This index is somewhat equivalent of the chromatic number for vertex coloring.

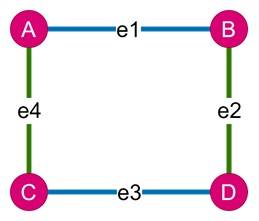
Here, the edges e1 and e3 are not sharing common vertex so they are in same color. The same logic applies to the edges e2 and e4.

Importance of Edge Coloring

Edge coloring is important in several situations where each edge represents a task or an event that needs unique timing or resource allocation. It is especially important when these tasks share common points or resources. It helps answer questions like, "How can we schedule tasks to avoid conflicts?" or "How many resources are necessary to prevent overlap?"

Practical Examples of Edge Coloring

Let us see some examples of edge coloring in real life.

Example of Chess Tournament Scheduling

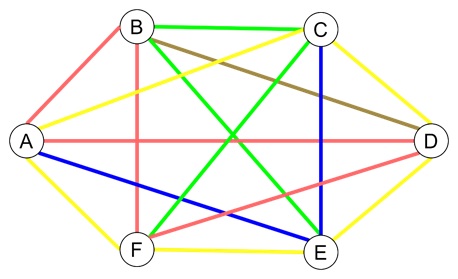
Consider a case where there are six friends who want to hold a chess tournament where each person plays against every other player. Now with limited chess sets, only one game can be played at a time by each person. Now the task is to determine the minimum number of time slots required for the tournament.

In graph terms, we can model each player as a vertex and each game as an edge. So for two players, who are scheduled to play each other, they are connected by an edge. We can understand that this will make a complete graph K₆ with six vertices. Since each player can play only one game per time slot, we need to understand that no two games are taking the same player are scheduled simultaneously.

To solve this, we will see the chromatic index of K₆. This will make out that five colors (or time slots) are enough to schedule all the games without overlap. It means the friends will need five hours to complete their tournament.

Chromatic Index and Vizings Theorem

There is an interesting theorem called the Vizing's Theorem. The Vizing's states to determine the chromatic index by offering a general rule. In this theorem for any graph G, the chromatic index χ′(G) is either equal to the maximum degree of the graph Δ(G) or Δ(G) + 1.

According to this theorem it is giving us a guideline for finding the minimum number of colors required in edge coloring. The theorem classifies graphs into two types:

• Class 1 Graphs − These graphs have a chromatic index of Δ(G).
• Class 2 Graphs − These graphs have a chromatic index of Δ(G) + 1.

While Vizing's Theorem gives this helpful range. It helps in determining whether a graph falls into Class 1 or Class 2. The process is not always straightforward. For instance, for bipartite graphs they belong to Class 1. It means they require only Δ(G) colors for edge coloring.

Example of Classroom Conflict Scheduling

Let us see the classroom example. Where we schedule classes. The scheduling has been done in such a way that certain classes cannot be held at the same time due to conflicts. These conflicts could be based on shared professors, rooms, or students enrolled in multiple classes. We can represent each class as an edge in a graph, where two edges share a vertex if their corresponding classes conflict.

Using the chromatic index of this conflict graph, we can find the minimum number of unique time slots needed to avoid overlap.

Ramsey Theory and Edge Coloring

Another interesting theory for edge coloring is Ramsey Theory. This is a branch of mathematics focused on finding order within chaos. In edge coloring, the Ramsey theory addresses questions about coloring edges in such a way that certain patterns are either created or avoided. For example, if every edge in a graph is colored either red or blue, can we avoid having any monochromatic triangles? These are the triangles where all edges are the same color.

Such questions are central to Ramsey Theory and become increasingly complex as we consider larger graphs or more colors. For example, research shows that avoiding a monochromatic triangle requires at least 17 vertices if three colors are used. The 18 vertices to avoid a monochromatic copy of K₄ using two colors.

Upper and Lower Bounds for Chromatic Index

Like the chromatic number bounds, chromatic index also have upper and lower bounds. These bounds help to estimate the minimum number of colors for proper edge coloring. It is particularly in large or complex graphs.

• Lower Bound − The chromatic index is always at least as large as the maximum degree of the graph, Δ(G). This is because, at minimum, each vertex's adjacent edges must be assigned unique colors.
• Upper Bound − Vizing's Theorem also shows the upper bound. χ′(G) is at most Δ(G) + 1. So, the chromatic index will always fall within the range Δ(G) ≤ χ′(G) ≤ Δ(G) + 1.

These bounds can simplify the edge-coloring problems. It will narrow down the potential range for the chromatic index before detailed coloring is applied.

Complexity of Finding Chromatic Index in Large Graphs

At the end if we talk about the complexity of the chromatic index finding we will face certain challenges. Finding the exact chromatic index in larger or more complex graphs can be computationally hard. Unlike some simpler graph problems, determining the chromatic index requires us to consider all potential colorings, especially in graphs that may fall close to the boundary of Vizings classification (between Class 1 and Class 2).

For practical applications, algorithms are used to approximate the chromatic index. However, these approximations are not always efficient or accurate. They are especially as the graph size increases. This complexity makes edge coloring an ongoing area of research.

Conclusion

In this chapter, we explained the concept of edge coloring in discrete mathematics. Starting with the basics, we covered the concept of chromatic index and understood its importance in assigning colors to graph edges. We presented some practical applications of edge coloring such as scheduling chess tournaments and resolving classroom conflicts etc.

We also discussed Vizings Theorem, which provides a helpful range for the chromatic index, and how it helps classify graphs as Class 1 or Class 2. Finally, we highlighted the Ramsey Theory, which explores edge coloring in the context of finding or avoiding specific patterns.