Principle of Inclusion and Exclusion in Discrete Mathematics

---

---

The Principle of Inclusion and Exclusion (PIE) is an important concept in Set Theory that helps in calculating the cardinality of the union of multiple sets; this is True even when those sets overlap. The basic idea is to include elements in the union but exclude those that have been counted multiple times with the overlapping sets. It is little bit complex at first, but we will break it down and understand how it works.

Principle of Inclusion and Exclusion

The Principle of Inclusion and Exclusion is useful for finding the size of the union of two or more sets. When these sets overlap, adding their sizes together this may lead to double-counting the elements. PIE corrects this by subtracting the sizes of the intersections. But if multiple intersections overlap, further adjustments are needed.

For two sets A and B, the union can be written as −

$$\mathrm{|A \:\cup\: B| \:=\: |A| \:+\: |B| \:-\: |A \:\cap\: B|}$$

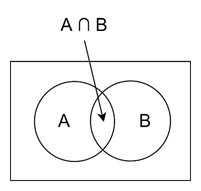
This formula works because the term $\mathrm{|A| \:+\: |B|}$ counts the elements in both sets. The intersection $\mathrm{|A \:\cap\: B|}$ gets counted twice. Once in A and once in B. By subtracting $\mathrm{|A \:\cap\: B|}$, we correct this overcounting.

Example of Two Sets

Let us look at an example. Suppose we have two sets −

• A is the set of students who like math, and there are 10 students in this set.
• B is the set of students who like science, and there are 8 students in this set.

The intersection A ∩ B, representing students who like both math and science, contains 6 students.

We want to know how many students like either math or science or both. Applying the formula:

$$\mathrm{|A \:\cup\: B| \:=\: |A| \:+\: |B| \:-\: |A \:\cap\: B| \:=\: 10 \:+\: 8 \:-\: 6 \:=\: 12}$$

Thus, 12 students like either math, science, or both.

Extending to Three Sets

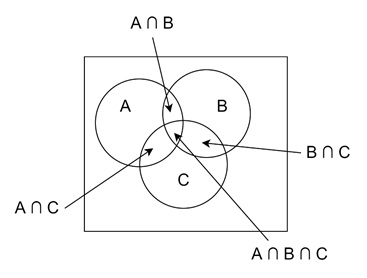
Let us extend this principle for three sets. The process becomes slightly more complex. The formula for the union of three sets A, B, and C is −

$$\mathrm{|A \:\cup\: B \:\cup \:C| \:=\: |A| \:+\: |B| \:+\: |C| \:-\: |A \:\cap\: B| \:-\: |A \:\cap\: C| \:-\: |B \:\cap\: C| \:+\: |A \:\cap\: B \:\cap\: C|}$$

This formula adds the sizes of the individual sets but subtracts the pairwise intersections to avoid double-counting. But, the triple intersection $\mathrm{|A \:\cap\: B \:\cap\: C|}$ gets subtracted three times. So we add it back in once.

Example of Three Sets

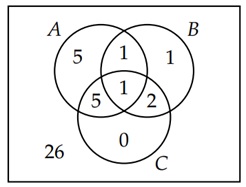
Consider the following example −

• A represents students who failed Algebra (12 students).
• B represents students who failed Biology (5 students).
• C represents students who failed Chemistry (8 students).
• There are 2 students who failed both Algebra and Biology,
• 6 who failed both Algebra and Chemistry,
• 3 who failed both Biology and Chemistry, and
• 1 student who failed all three subjects.

We want to find the number of students that failed at least one subject. Using the formula for three sets −

$$\mathrm{|A \:\cup\: B \:\cup\: C| \:=\: |A| \:+\: |B| \:+\: |C| \:-\: |A \:\cap\: B| \:-\: |A \:\cap\: C| \:-\: |B\: \cap\: C| \:+\: |A \:\cap\: B \:\cap\: C|}$$

$$\mathrm{|A \:\cup\: B \:\cup\: C| \:=\: 12 \:+\: 5 \:+\: 8 \:-\: 2 \:-\: 6 \:-\: 3 \:+\: 1 \:=\: 15}$$

So, 15 students failed at least one subject.

General Formula for n Sets

The Principle of Inclusion and Exclusion can be generalized for any number of sets. For instance, if we have n sets (A₁, A₂, …, A_n) the size of their union is given by −

$$\mathrm{|A_1 \:\cup\: A_2 \:\cup\: \dots \:\cup\: A_n| \:= \:\sum_{i=1}^n |A_i| \:-\: \sum_{1 \:\leq\: i \:\lt\: j \:\leq\: n} |A_i \:\cap\: A_j| \:+\: \sum_{1 \:\leq\: i \:\lt\: j \:\lt\: k \:\leq\: n} |A_i \:\cap\: A_j \:\cap\: A_k| \:-\: \dots}$$

The formula alternates between adding and subtracting. This is because intersections of increasing size.

An Example with Four Sets

Let us look at a slightly more complicated example with four sets.

A school is hosting an event. Here students can sign up for four different activities: football, badminton, hockey, and cricket.

• 30 students signed up for football.
• 25 students signed up for badminton.
• 20 students signed up for hockey.
• 15 students signed up for cricket.
• 10 students signed up for both football and badminton.
• 8 students signed up for both football and hockey.
• 5 students signed up for both football and cricket.
• 7 students signed up for both badminton and hockey.
• 4 students signed up for both badminton and cricket.
• 6 students signed up for both hockey and cricket.
• 3 students signed up for all four activities.

To find how many students are signed up for at least one activity, we can apply the Principle of Inclusion and Exclusion. Here the formula becomes more complicated with four sets. It is useful to break down the terms step by step. But in the end, using PIE helps us avoid counting the students multiple times.

Applications of Inclusion and Exclusion

The Principle of Inclusion and Exclusion is not just a theoretical tool. It has several practical applications, including −

• Counting Problems − When trying to count the number of elements that meet at least one criterion.
• Probability − It helps calculate the probability of the union of several events by correcting for overlapping events.
• Computer Science − Algorithms often use PIE to count specific combinations of data structures like sets, graphs, or networks.

Conclusion

In this chapter, we explained the Principle of Inclusion and Exclusion (in short PIE) in discrete mathematics. We started by discussing the basics, including how the principle works for two sets. We then moved on to three sets, showing how the formula becomes more complex but still follows the same core idea.

We used an example to demonstrate how to use the principle to count students in different activities or subjects. Finally, we presented the general formula for any number of sets and how the principle is applied in counting, probability, and computer science.