
- Discrete Mathematics - Home
- Discrete Mathematics Introduction
- Mathematical Statements and Operations
- Atomic and Molecular Statements
- Implications
- Predicates and Quantifiers
- Sets
- Sets and Notations
- Relations
- Operations on Sets
- Venn Diagrams on Sets
- Functions
- Surjection and Bijection Functions
- Image and Inverse-Image
- Mathematical Logic
- Propositional Logic
- Logical Equivalence
- Deductions
- Predicate Logic
- Proof by Contrapositive
- Proof by Contradiction
- Proof by Cases
- Rules of Inference
- Group Theory
- Operators & Postulates
- Group Theory
- Algebric Structure for Groups
- Abelian Group
- Semi Group
- Monoid
- Rings and Subring
- Properties of Rings
- Integral Domain
- Fields
- Counting & Probability
- Counting Theory
- Combinatorics
- Additive and Multiplicative Principles
- Counting with Sets
- Inclusion and Exclusion
- Bit Strings
- Lattice Path
- Binomial Coefficients
- Pascal's Triangle
- Permutations and Combinations
- Pigeonhole Principle
- Probability Theory
- Probability
- Sample Space, Outcomes, Events
- Conditional Probability and Independence
- Random Variables in Probability Theory
- Distribution Functions in Probability Theory
- Variance and Standard Deviation
- Mathematical & Recurrence
- Mathematical Induction
- Formalizing Proofs for Mathematical Induction
- Strong and Weak Induction
- Recurrence Relation
- Linear Recurrence Relations
- Non-Homogeneous Recurrence Relations
- Solving Recurrence Relations
- Master's Theorem
- Generating Functions
- Graph Theory
- Graph & Graph Models
- More on Graphs
- Planar Graphs
- Non-Planar Graphs
- Polyhedra
- Introduction to Trees
- Properties of Trees
- Rooted and Unrooted Trees
- Spanning Trees
- Graph Coloring
- Coloring Theory in General
- Coloring Edges
- Euler Paths and Circuits
- Hamiltonion Path
- Boolean Algebra
- Boolean Expressions & Functions
- Simplification of Boolean Functions
- Advanced Topics
- Number Theory
- Divisibility
- Remainder Classes
- Properties of Congruence
- Solving Linear Diophantine Equation
- Useful Resources
- Quick Guide
- Useful Resources
- Discussion
Rooted and Unrooted Trees in Discrete Mathematics
Trees are special structures in graph theory and discrete mathematics. Trees are used for representing hierarchies and connections without cycles. The rooted and unrooted trees gives us two different ways to structure and interpret such data.
In this chapter, we will see rooted and unrooted trees. Their characteristics, examples, and applications. We will see the key differences and use examples to highlight each types properties for a better understanding.
Trees in Graph Theory
In graph theory, a tree is a type of connected graph that has no cycles. Each node in the tree represents an entity, and each edge represents a connection between entities.
Trees can be structured in various ways. We can categorize them as either rooted or unrooted depending on their structure and use.
- Unrooted Trees − These are trees with no designated root or starting point. All vertices in unrooted trees are equally important without any hierarchy.
- Rooted Trees − In contrast, a rooted tree designates one vertex as the “root”. This vertex serves as a reference point for organizing all other vertices hierarchically.
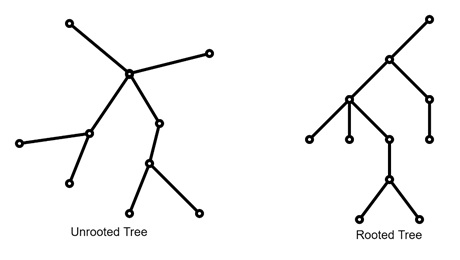
Unrooted Trees
Unrooted trees are such structures with no clear hierarchy or direction. This type of tree is common in data representations and does not require a central or “starting” point.
Properties of Unrooted Trees
Let us see some of the properties of unrooted trees. There is node without any specific node serving as a reference. In unrooted trees, each edge represents a connection with no particular order.
Example
Consider a network of cities connected by roads where the only requirement is to connect all cities without any cycles (circular routes). In this case, an unrooted tree could be used to represent the network. Here, each city is connected to at least one other. This ensuring a unique path exists between each pair without loops.
Applications of Unrooted Trees
The unrooted trees are used in scenarios where the structure does not need a hierarchical organization, like −
- Phylogenetic Trees − In biology, unrooted phylogenetic trees represent evolutionary relationships between species without assuming a common ancestor.
- Network Design − Designing computer networks where devices connect without a central hub is another example. In this setup, unrooted trees ensure redundancy and connectivity without a hierarchical structure.
Rooted Trees
We have another type of trees. The rooted trees. It has a clear hierarchy by selecting one vertex as the root. This root acts as an anchor, giving a structured way to organize the vertices.
Structure of Rooted Trees
In a rooted tree, the relationships are organized based on proximity to the root. Each node can have child nodes, and each node except the root has exactly one parent. So there is a parent-child relationship. Like a family tree or an organizational chart.
- Parent-Child Relationship − In a rooted tree, if two vertices are connected by an edge, one is designated as the parent and the other as the child. The child node is "downward" from the parent.
- Siblings − Vertices that share the same parent are siblings.
- Ancestors and Descendants − In this tree structure, nodes can have ancestors (nodes closer to the root) and descendants (nodes further from the root).
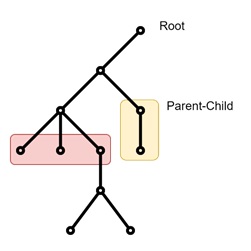
Example
Consider a corporate hierarchy where the CEO is at the top. And each department head reports to the CEO, and each department head has employees reporting to them. So the CEO serves as the root. There are department heads as children, and employees under each department head as grandchildren of the root.
Properties of Levels and Depths
Vertices are grouped into levels based on their distance from the root, with the root being at level 0. Each level represents a step down in hierarchy, and the number of levels can determine the trees depth.
Example
Consider a binary tree with three levels. The root is at level 0, its children are at level 1, and so on. This structure is there to give the vertices are systematically organized. They are making it easy to trace paths up or down the hierarchy.
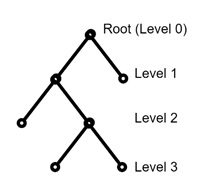
Algorithms and Traversal in Rooted Trees
One of the primary reasons the rooted trees are useful is their ease of traversal. Traversal means visiting each vertex in a specific order.
- Breadth-First Search (BFS) − The basic traversal is BFS. It starts at the root and visits all vertices level by level. This is like reading a book chapter by chapter, where each chapter (or level) is read fully before moving to the next.
- Depth-First Search (DFS) − Another one is It goes as far down one path as possible before backtracking. This method is like exploring a family tree by tracing one lineage from great-grandparents down to current generations before looking at other branches.
Difference between Rooted and Unrooted Trees
Rooted and unrooted trees have several differences because of their structures. Let us see them in the following table −
| Feature | Rooted Tree | Unrooted Tree |
|---|---|---|
| Root Node | Has a designated root node | No root node |
| Hierarchy | Hierarchical structure | Non-hierarchical |
| Traversals | BFS, DFS (based on the root) | No specific traversal order |
| Applications | File systems, corporate structures | Phylogenetic trees, non-hierarchical networks |
Real-World Applications of Rooted and Unrooted Trees
Rooted and unrooted trees have many such applications in computer science, biology, and network theory.
- Rooted Trees in Web Design − In web design, rooted trees organize web pages by hierarchy. For example, a website might start with the homepage as the root, with main sections branching off, and each section containing more specific subpages.
- Unrooted Trees in Biology − Unrooted trees often represent relationships in biology, such as between species that share similar characteristics but do not necessarily have a single common ancestor. This helps biologists understand similarities without assuming a direct lineage.
Rooted and Unrooted Trees in Data Organization
When organizing data, rooted and unrooted trees each have distinct advantages −
- Rooted Trees for Data Hierarchies − When data requires a clear organization from top to bottom, such as in XML files. The root provides a starting point. This is making it easy to navigate through structured layers.
- Unrooted Trees for Relational Data − If the data does not require hierarchy, the unrooted trees offer flexibility by showing relationships without emphasizing a central point.
For example, a computer file system uses rooted trees to allow users to follow a single path from the main directory to each file. On the other hand, a social network might use an unrooted tree to make mutual friendships without implying a hierarchy.
Conclusion
In this chapter, we explained the features of rooted and unrooted trees, based on their structures and applications. Rooted trees provide a hierarchical model that is ideal for situations where organization and levels matter.
We also understood how unrooted trees are effective in scenarios without a central point, like phylogenetic trees. In addition, we touched upon some basic traversal techniques in rooted trees such as BFS and DFS.