Polyhedra in Discrete Mathematics

---

---

Polyhedra are three-dimensional solids that are used in both geometry and discrete mathematics. These shapes are flat polygonal faces with straight edges and sharp vertices. Polyhedra are special shapes and they offer a way to explore the properties of space, structure, and symmetry.

In this chapter, we will see the basics of polyhedra and understand some of its most well-known types.

What is a Polyhedron?

A polyhedron is a three-dimensional shape with flat faces. Each one being a polygon. Every face meets other faces along edges, and these edges connect at vertices. We can see polyhedra all around us, from dice to crystals. They provide practical examples of geometrical and mathematical concepts.

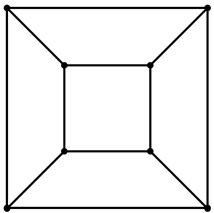
In discrete mathematics, we focus on the structure and properties of polyhedral. Our major focus is on convex and regular polyhedra.

Convex Polyhedra

A polyhedron is convex if any line segment drawn between two points within it stays entirely inside the polyhedron. Like cube or a pyramid. Any line we draw from one point inside to another point inside will not leave the shape.

A convex polyhedron is simpler to analyze because it does not "bend inwards". They are useful in making calculations and theoretical explorations more straightforward.

Regular Polyhedra

When each face of a polyhedron is identical and every vertex connects the same number of edges, we call it a regular polyhedron.

In fact, there are only five polyhedra that fit this exact definition. These are the Platonic solids.

Each Platonic solid has faces that are regular polygons (like triangles or squares), and each vertex joins the same number of faces. Let us see these five unique shapes.

The Five Platonic Solids

The five Platonic solids are −

• Tetrahedron − 4 triangular faces
• Cube (or Hexahedron) − 6 square faces
• Octahedron − 8 triangular faces
• Dodecahedron − 12 pentagonal faces
• Icosahedron − 20 triangular faces

These shapes are special because they are the only convex polyhedra where each face is the same polygon and each vertex joins the same number of faces. The symmetry and regularity of Platonic solids make them important in both math and nature. It may think of how molecules form or how crystals grow.

Eulers Formula for Polyhedra

The Eulers formula is a simple yet powerful equation that connects the number of vertices, edges, and faces of a polyhedron.

For any convex polyhedron, Eulers formula states −

$$\mathrm{v \:-\: e \:+\: f \:=\: 2}$$

where −

• v is the number of vertices
• e is the number of edges
• f is the number of faces

Applying Euler's Formula

To see how Euler's formula works, let us see it to a familiar shape: the cube.

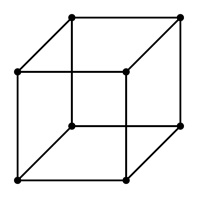
A cube has 8 vertices, 12 edges, and 6 faces.

Plugging these values into Euler's formula −

$$\mathrm{8 \:-\: 12 \:+\: 6 \:=\: 2}$$

Eulers formula is holding. This formula provides a reliable way to check the structure of any convex polyhedron and applies to each of the five Platonic solids.

How Does Eulers Formula Work?

The Eulers formula reflects the topological nature of convex polyhedra. Even if we project a polyhedron onto a two-dimensional plane, the formula holds.

Consider wrapping a polyhedron in a sphere, then stretching it out flat. The Eulers formula still applies because it captures the relationships among vertices, edges, and faces.

Examples and Explorations with Polyhedra

Let us see some examples to see how Eulers formula and other properties apply to different types of polyhedra.

Example 1: The Octahedron

Take a look at the following polyhedron −

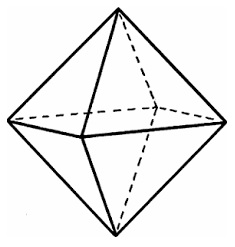
The octahedron has:

• Vertices (v): 6,
• Edges (e): 12,
• Faces (f): 8.

Using Euler's formula, we confirm −

$$\mathrm{6 \:-\: 12 \:+\: 8 \:=\: 2}$$

So the octahedron has triangular faces, and each vertex connects four edges. It is forming a highly symmetrical shape. In fact, an octahedron has the same number of edges as a cube. The difference is in how these edges and faces are arranged. It is showing the diverse forms polyhedra which can take even when they share the same edge count.

Example 2: Is There a Polyhedron with Three Triangles and Six Pentagons?

Imagine we want to know if we can make a polyhedron made of three triangles and six pentagons. To figure this out, we can use edge calculations.

The triangles will give a total of 9 edges, and the pentagons would contribute 30 edges.

Each edge, however, would be counted twice (since each edge borders two faces). This gives a total of (9 + 30) / 2 = 19.5 edges.

This fractional result makes no sense in a physical object, so no such polyhedron could exist.

Example 3: Another Hypothetical Polyhedron with Additional Faces

Consider we try adding five heptagonal faces (7-sided polygons) to the structure in Example 2.

We have three triangles, six pentagons, and five heptagons. The triangles contribute 9 edges, the pentagons 30, and the heptagons 35 edges.

Dividing by 2 again, we find the total number of edges would be (9 + 30 + 35) / 2 = 37, which can theoretically work.

However, when we apply Euler's formula, we discover that, while the edge count fits, other vertex requirements cannot be met due to the degree constraints at each vertex. So such a polyhedron is impossible to construct.

Polyhedra and Graph Theory

In graph theory, a polyhedron can be represented as a graph. Here vertices, edges, and faces correspond to graph nodes, connections, and regions respectively. This relationship allows mathematicians to study polyhedra using planar graphs.

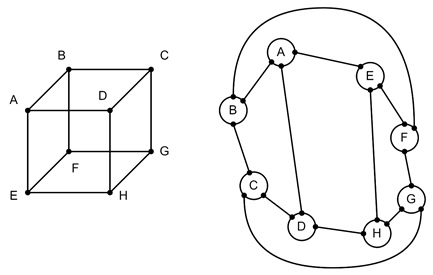
Projecting Polyhedra onto a Plane

Each polyhedron can be projected onto a plane, and it is a planar graph. This projection gives a graph representation that maintains the relationships among vertices, edges, and faces.

For example, a cube can be drawn as a network of vertices and edges on a plane, showing how polyhedra relate to planar graph structures.

Applications of Polyhedra

Polyhedra is showing up in various areas of science. From biology to architecture. There are a few applications where polyhedra play a role −

• Molecular Structure − Polyhedral shapes appear in molecular formations, where atoms group in regular patterns, like in carbon molecules.
• Crystallography − Many crystals form polyhedral structures, revealing natural symmetry.
• Architecture − In construction, polyhedral shapes, especially tetrahedrons and octahedrons, are used to create strong, stable frameworks.

Polyhedra is used to understand and apply geometric principles in real-world contexts.

Conclusion

In this chapter, we explained the basic concepts of polyhedra and considered its key types such as convex and regular polyhedra.

The five Platonic solids are unique due to their regularity and symmetry. We applied Eulers formula to analyze their properties and used graph theory concepts to project polyhedra onto a plane. Additionally, we demonstrated why only five Platonic solids exist. Through examples, we explored both possible and impossible polyhedral structures.