Hamiltonian Path in Discrete Mathematics

---

---

The Hamiltonian path is a path that visits every vertex in a graph exactly once. This is named after the Irish mathematician Sir William Rowan Hamilton. The concept is quite useful in areas like circuit design, puzzle solving, and optimization in route planning.

In this chapter, we will see the important concepts of Hamiltonian paths, including its definition, examples, and insights into finding them in graphs.

Hamiltonian Path

Hamiltonian path in a graph is just a path that passes through every vertex exactly once. This is not like Euler paths. These are concerned with traversing each edge.

Hamiltonian paths focus on covering all the vertices. If we consider an example of visiting each city in a network map without revisiting any; a Hamiltonian path would represent the exact sequence of stops.

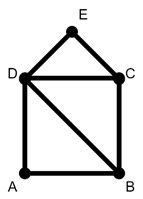
The Hamiltonian path could be ADECB. We do not need to traverse all edges.

Hamiltonian Cycle

A Hamiltonian cycle (or Hamiltonian circuit) is similar to a Hamiltonian path but there is one crucial difference: it starts and ends at the same vertex. And it is forming a closed loop. If there is a route that lets we visit each location once and then return to the starting point, we have completed a Hamiltonian cycle.

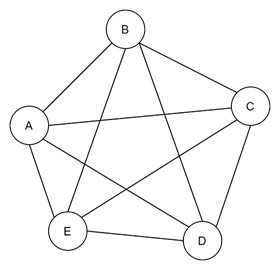
For this, we can follow ABCDEA as the Hamiltonian cycle.

Conditions and Properties of Hamiltonian Paths and Cycles

In the first impression, the Hamiltonian paths looks very simple. It does not have a simple rule like the degree-based conditions found in Euler paths. Here, the degree of each vertex can determine the existence of a path or circuit.

The Hamiltonian paths depend on a variety of factors, like graph size, structure, and symmetry.

• Connected Graphs − For a graph where Hamiltonian path to exist, the graph must be connected; so that all vertices should be accessible.
• Cycle-Friendly Structure − Graphs that are "cycle-friendly" (where cycles can naturally form) are often more likely to have Hamiltonian paths or cycles.

Hamiltonian Graphs and Complexity

A graph that has a Hamiltonian cycle is called a Hamiltonian graph. But checking these graphs is not such straightforward process. This is computationally hard. If the size grows this falls into a category known as NP-complete problems.

So, as far as we know, there are no quick ways to find a solution. This complexity is why Hamiltonian paths are studied both theoretically and practically.

Example 1: Simple Hamiltonian Path in a Graph

Consider a simple linear graph with four vertices arranged in a line: A, B, C, and D. It is connected sequentially (A-B, B-C, and C-D).

Since the graph is a single line, there is a clear Hamiltonian path that starts at A, visits B, then C, and finally reaches D. This is covering all vertices exactly once. This graph has a Hamiltonian path (A to D) but not a Hamiltonian cycle because there is no way to return from D to A without retracing edges.

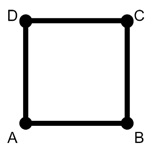
Example 2: A Square Graph with a Hamiltonian Cycle

Let us now take a square with vertices A, B, C, and D connected in a loop. Here, we can start at A, go to B, then C, then D, and finally return to A. This cycle covers each vertex once and ends at the starting point. This is forming a Hamiltonian cycle. This graph is a Hamiltonian graph since it has a Hamiltonian cycle.

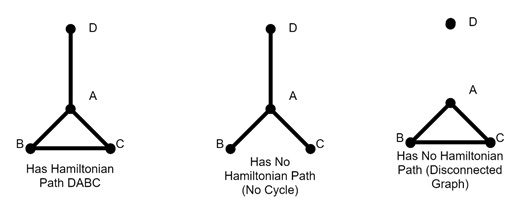
Example 3: A Graph without a Hamiltonian Path

Not all graphs allow for a Hamiltonian path. Consider a graph shaped like a "star," with a central vertex connected to multiple outer vertices. This structure has no way to visit each vertex exactly once. It is without missing or revisiting vertices, which makes a Hamiltonian path impossible.

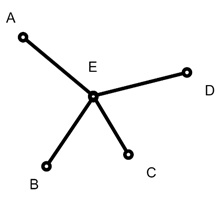
The Complexity of Checking Paths

Unlike Euler paths, where rules about vertex degree simplify finding paths. For Hamiltonian path, there is no straightforward test for Hamiltonian paths. As a result, identifying Hamiltonian paths or cycles can be time-consuming. This is like in large graphs. For small graphs, one might be able to manually test each possible route. But this method is impractical for anything substantial.

Real-World Applications of Hamiltonian Path

Hamiltonian paths has several real-world applications in many problems −

• Traveling Salesperson Problem (TSP) − In TSP, a salesperson needs to visit a set of cities and return to the starting city. The challenge is to find the shortest possible route that visits each city once. This is a perfect example of finding a Hamiltonian cycle.
• DNA Sequencing − In bioinformatics, DNA sequencing sometimes involves finding Hamiltonian paths in graphs to reconstruct sequences from fragments.

Common Misunderstandings about Hamiltonian Paths

Confusion between Hamiltonian and Euler Paths − It is easy to confuse Hamiltonian paths with Euler paths. If we rethink, the Hamiltonian paths aim to visit each vertex once. The Euler paths focus on covering each edge once. Both are concerned with unique coverage but differ in their focus on vertices versus edges.

Assuming All Connected Graphs Have Hamiltonian Paths − Another confusing thing is when a graph is connected, it does not necessarily need to have a Hamiltonian path. For instance, a star graph is connected but has no Hamiltonian path. So, connectivity alone does not guarantee a Hamiltonian path or cycle.

Conclusion

In this chapter, we explained the concept of Hamiltonian paths in discrete mathematics. We covered the basics of what defines a Hamiltonian path and a Hamiltonian cycle. We discussed their unique conditions and challenges, and saw examples of when these paths and cycles appear in different graph types.

Additionally, we also touched upon some real-world applications like the Traveling Salesperson Problem and DNA sequencing.