Surjection, Injection and Bijection Function

---

---

Functions are nothing but mapping relationships between different sets. To fully understand functions, we need to understand three key concepts: surjection, injection, and bijection. In this chapter, we will see each of these function types with examples and see how they differ from one another.

Functions in Sets and Relations

A function is a rule that takes elements from one set (domain) and assigns them to elements in another set (codomain). Every element in the domain must map to exactly one element in the codomain. However, the reverse is not necessarily true. For example, imagine we assign every student in a class a locker. Each student gets exactly one locker, but some lockers may remain unused.

Here is another example. Take a look at the following mapping: Here, each number from left has a square on the right −

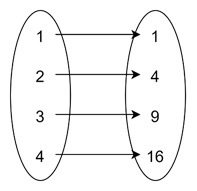
Surjection Functions That Are "Onto"

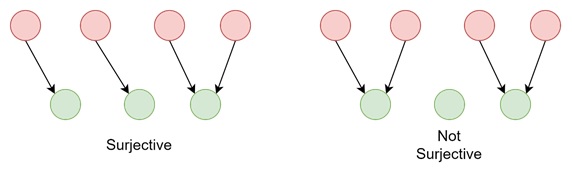
A surjective function, also known as an "onto" function. It is a function where every element in the codomain is the image of at least one element in the domain. In simpler words, there are no unused elements in the codomain.

Formally, a function is surjective if every element of the codomain is the image of at least one element from the domain. Nothing in the codomain is left out.

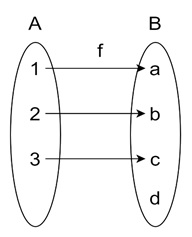
Example of Surjection

Let us consider the function f : {1, 2, 3} → {a, b, c} defined by: f(1) = a, f(2) = b, f(3) = c

Here, every element in the codomain {a, b, c} has been "hit" by some element from the domain {1, 2, 3}. This means f is a surjective function because there are no elements left out in the codomain.

The following mapping presents another example −

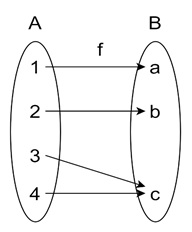
Example of Non-Surjective

Now, consider a function g : {1, 2, 3} → {a, b, c} where: g(1) = a, g(2) = a, g(3) = c.

In this case, the element b from the codomain is never "hit" by any element from the domain. This means g is not surjective because something in the codomain is left out.

Surjections are important when we want to ensure that every possible output is covered. There is no leaving "gaps."

Injection Functions That Are "One-to-One"

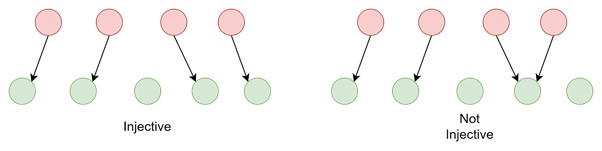
On the other hand, the injective function, or "one-to-one" function, shows that no two different elements in the domain map to the same element in the codomain. This means every element in the codomain is the image of at most one element in the domain.

Formally, a function is injective if every element of the codomain is the image of at most one element from the domain. There are no "repeated" images in the codomain.

Example of Injection

Let us consider f : Z → Z (where Z represents all integers) is defined by: f(n) = 3n

For every integer n, f(n) produces a unique result. No two different integers will give the same value after being multiplied by 3. Therefore, this function is injective. It does not "reuse" codomain elements for different domain inputs.

Example of Non-Injective

Consider a function h : {1, 2, 3} → {a, b} defined by: h(1) = a, h(2) = a, h(3) = b

In this case, both h(1) and h(2) are mapped to a. Since two different domain elements are assigned to the same codomain element, h is not injective. Injection fails when there is "overlap" in the codomain.

Bijection The Perfect Function

Next comes the bijection functions. It is both injective and surjective. In other words, every element in the domain maps to a unique element in the codomain, and every element in the codomain is covered. This makes bijections "perfect" functions because they pair every element in the domain with one (and only one) element in the codomain, with no repeats and no leftovers.

Formally, a function is bijective if it is both injective and surjective, meaning it’s a one-to-one correspondence between the domain and codomain.

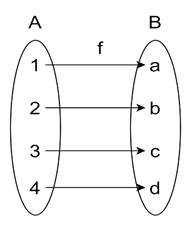
Example of Bijection

Consider the function f : {1, 2, 3} → {a, b, c}, defined as: f(1) = a, f(2) = b, f(3) = c.

This is a bijection because every element in the domain has a unique match in the codomain, and every codomain element is used. There are no repeated values and no leftover elements.

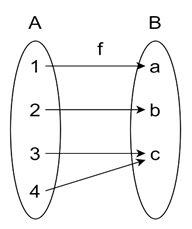
Example of Non-Bijective Function

If we modify f such that f(2) = a, then the function is no longer bijective. It might still be surjective (depending on the other values), but it is no longer injective because two elements in the domain share the same codomain value.

Combining Concepts: Injective vs Surjective

We understood the idea of injective and surjective. But these are essential to understand that injective and surjective functions are not opposites.

A function can be injective but not surjective; surjective but not injective; both; or neither.

• A function can be injective but miss out some elements in the codomain, making it not surjective.
• A function can be surjective but reuse elements of the codomain, making it not injective.
• A bijection is both injective and surjective, satisfying both properties.

Conclusion

In this chapter, we explained the concept of surjection, injection, and bijection functions in discrete mathematics. Surjection functions cover every element in the codomain. Injection functions avoid reusing codomain elements. Bijection functions do both. We also touched on inverse functions and how they only exist for bijections.