Euler Paths and Circuits in Discrete Mathematics

---

---

Euler paths and circuits are the most fundamental concepts in Graph Theory. With these concepts, we can solve real-world problems like network traversal, delivering mail along a specific route, planning circuits, etc. We study Euler paths and circuits to understand how we can traverse each edge in a graph, visiting each path once.

Read this chapter to learn the basics of Euler paths and circuits and understand the core properties of graphs that allow for these paths and circuits.

What is an Euler Path?

An Euler path is nothing but a graph that is a sequence where every edge is visited exactly once. In simple terms, if we have a map with roads represented as edges and intersections as vertices, the Euler path gives provision to travel along every road without backtracking. But here, we do not need to return to the starting point in an Euler path.

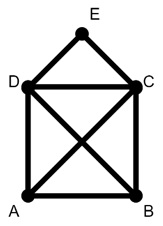
If we follow the path ABCEDCADB, it will form this graph without repeating same edges twice.

What is an Euler Circuit?

An Euler circuit is a special type of Euler path. It starts and ends at the same vertex. Like the Euler path, it traverses each edge only once. This closed-loop feature of the Euler circuit makes it unique from an Euler path. We can think of it like a postal route that starts at the post office, covers every street once, and returns to the starting point.

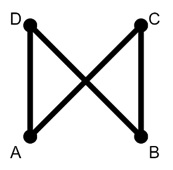
If we follow ACBDA, we will form the graph and also reach A again.

Conditions for Euler Paths and Circuits

Whether a graph has an Euler path or circuit it is depending on specific properties. They are related to vertex degree (the number of edges connected to a vertex).

• Euler Path − A graph will have an Euler path if it has exactly two vertices with an odd degree. So the path will start at one of these vertices and end at the other.
• Euler Circuit − A graph will have an Euler circuit if every vertex in the graph has an even degree. So we can start at any vertex and return to it after covering every edge once.

These conditions give a quick way to check if a graph has an Euler path or circuit without needing to test every possible route manually.

The Bridges of Knigsberg Problem

The Bridges of Knigsberg problem is one of the most frequently used examples in graph theory. The problem kept the citizens of Knigsberg (now Kaliningrad, Russia) puzzled for years. The city had seven bridges connecting different lands. The people wanted to know if it was possible to walk through the city crossing each bridge exactly once.

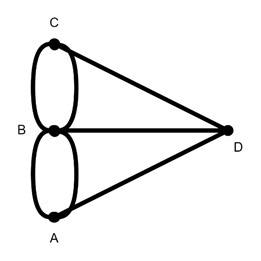
Representing this problem as a graph, it turns out the graph had more than two vertices with an odd degree, so no Euler path or circuit exists. This insight, discovered by mathematician Leonhard Euler, marked the birth of graph theory.

Simple Euler Path

Consider a graph with four vertices arranged in a straight line (A, B, C, and D) like below −

• Vertices A and D have a degree of 1 (odd).
• Vertices B and C have a degree of 2 (even).

So there are exactly two vertices (A and D) with an odd degree, and we have an Euler path here. The path can start at A, traverse each edge, and end at D. We can also start from D to end at A covering every edge without repetition.

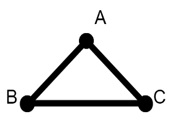
Simple Euler Circuit

Consider a triangle graph where each vertex is connected to the other two (forming a cycle). Here each of the three vertices here has a degree of 2 (even), fulfilling the condition for an Euler circuit. So starting from any vertex, we can travel through each edge once and return to the starting vertex.

Visualizing Degrees and Paths

Dead Ends and Odd Degrees − In a graph, a vertex with a degree of 1 can become a dead end. And this will prevents an Euler circuit. For example, if there is a spike extending from one vertex in a closed network, the graph will have at least one vertex with an odd degree. This will break the condition for an Euler circuit.

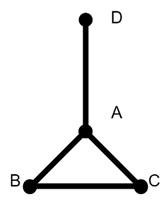
Balancing Inbound and Outbound Edges

For an Euler circuit to exist, every time we arrive at a vertex, we should have a way to leave it. It explains why all vertices need an even degree. A vertex with an odd degree will leave us stranded because there will be an unpaired edge we cannot use without repeating an edge.

Identifying Euler Paths and Circuits

Counting Odd Degrees − To determine whether a graph has an Euler path or circuit, we need to list the degree (number of edges) for each vertex. Then, count how many vertices have an odd degree.

• If exactly two vertices have an odd degree, there is an Euler path.
• If all vertices have an even degree, there is an Euler circuit.
• If more than two vertices have an odd degree, neither an Euler path nor circuit exists.

Applications of Euler Paths and Circuits

Euler paths and circuits have practical applications in areas like logistics, network design, and even DNA sequencing.

Postal and Garbage Collection Routes

Consider a postal worker who wants to cover every street in a neighborhood without retracing steps. By organizing the neighborhood as a graph, an Euler circuit gives the path the worker can complete the route efficiently if every street connection (vertex degree) is even.

Similarly, garbage collection routes and road maintenance planning too rely on this logic for efficient traversal.

DNA Sequencing

In computational biology, Euler paths help assemble DNA sequences by treating fragments of DNA. This is as edges and overlaps as vertices. An Euler path through this graph reconstructs the original DNA sequence.

Conclusion

In this chapter, we explained the basics of Euler paths and circuits in graph theory. We understood the differences of an Euler path from an Euler circuit. We discussed the conditions that allow for their existence.

In addition, we presented the practical applications of Euler paths and circuits, from postal routes to DNA sequencing, showing the value of these mathematical concepts in real-world situations.