
- Discrete Mathematics - Home
- Discrete Mathematics Introduction
- Mathematical Statements and Operations
- Atomic and Molecular Statements
- Implications
- Predicates and Quantifiers
- Sets
- Sets and Notations
- Relations
- Operations on Sets
- Venn Diagrams on Sets
- Functions
- Surjection and Bijection Functions
- Image and Inverse-Image
- Mathematical Logic
- Propositional Logic
- Logical Equivalence
- Deductions
- Predicate Logic
- Proof by Contrapositive
- Proof by Contradiction
- Proof by Cases
- Rules of Inference
- Group Theory
- Operators & Postulates
- Group Theory
- Algebric Structure for Groups
- Abelian Group
- Semi Group
- Monoid
- Rings and Subring
- Properties of Rings
- Integral Domain
- Fields
- Counting & Probability
- Counting Theory
- Combinatorics
- Additive and Multiplicative Principles
- Counting with Sets
- Inclusion and Exclusion
- Bit Strings
- Lattice Path
- Binomial Coefficients
- Pascal's Triangle
- Permutations and Combinations
- Pigeonhole Principle
- Probability Theory
- Probability
- Sample Space, Outcomes, Events
- Conditional Probability and Independence
- Random Variables in Probability Theory
- Distribution Functions in Probability Theory
- Variance and Standard Deviation
- Mathematical & Recurrence
- Mathematical Induction
- Formalizing Proofs for Mathematical Induction
- Strong and Weak Induction
- Recurrence Relation
- Linear Recurrence Relations
- Non-Homogeneous Recurrence Relations
- Solving Recurrence Relations
- Master's Theorem
- Generating Functions
- Graph Theory
- Graph & Graph Models
- More on Graphs
- Planar Graphs
- Non-Planar Graphs
- Polyhedra
- Introduction to Trees
- Properties of Trees
- Rooted and Unrooted Trees
- Spanning Trees
- Graph Coloring
- Coloring Theory in General
- Coloring Edges
- Euler Paths and Circuits
- Hamiltonion Path
- Boolean Algebra
- Boolean Expressions & Functions
- Simplification of Boolean Functions
- Advanced Topics
- Number Theory
- Divisibility
- Remainder Classes
- Properties of Congruence
- Solving Linear Diophantine Equation
- Useful Resources
- Quick Guide
- Useful Resources
- Discussion
Discrete Mathematics - Spanning Trees
A spanning tree of a connected undirected graph $G$ is a tree that minimally includes all of the vertices of $G$. A graph may have many spanning trees.
Example
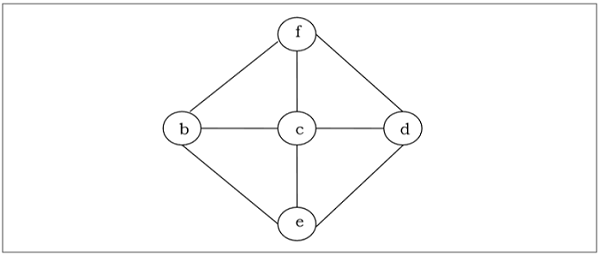
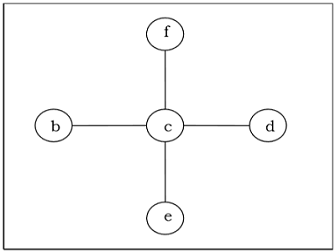
Minimum Spanning Tree
A spanning tree with assigned weight less than or equal to the weight of every possible spanning tree of a weighted, connected and undirected graph $G$, it is called minimum spanning tree (MST). The weight of a spanning tree is the sum of all the weights assigned to each edge of the spanning tree.
Example
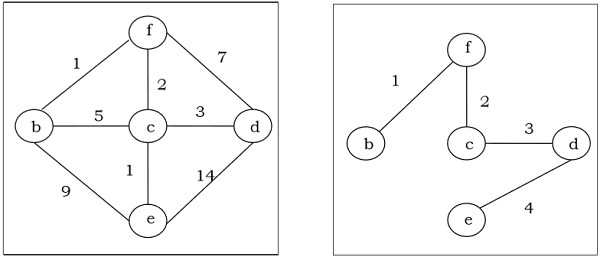
Kruskal's Algorithm
Kruskal's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted graph. It finds a tree of that graph which includes every vertex and the total weight of all the edges in the tree is less than or equal to every possible spanning tree.
Algorithm
Step 1 − Arrange all the edges of the given graph $G (V,E)$ in ascending order as per their edge weight.
Step 2 − Choose the smallest weighted edge from the graph and check if it forms a cycle with the spanning tree formed so far.
Step 3 − If there is no cycle, include this edge to the spanning tree else discard it.
Step 4 − Repeat Step 2 and Step 3 until $(V-1)$ number of edges are left in the spanning tree.
Problem
Suppose we want to find minimum spanning tree for the following graph G using Kruskals algorithm.
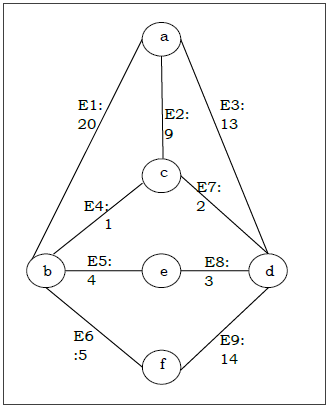
Solution
From the above graph we construct the following table −
| Edge No. | Vertex Pair | Edge Weight |
|---|---|---|
| E1 | (a, b) | 20 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E4 | (b, c) | 1 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
Now we will rearrange the table in ascending order with respect to Edge weight −
| Edge No. | Vertex Pair | Edge Weight |
|---|---|---|
| E4 | (b, c) | 1 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
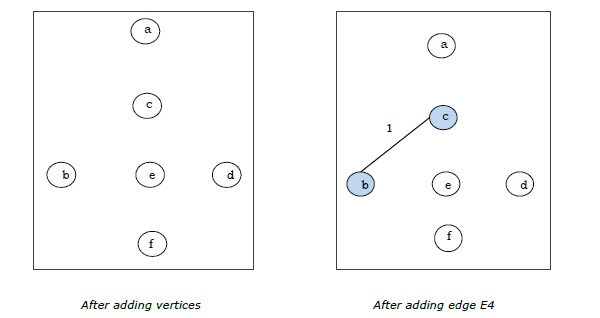
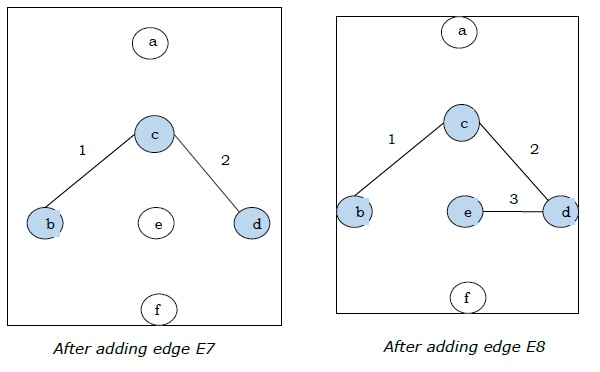
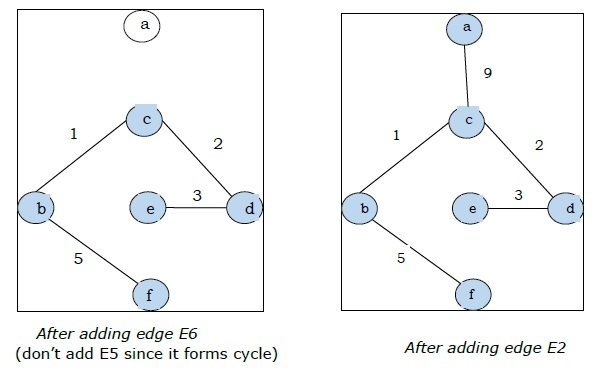
Since we got all the 5 edges in the last figure, we stop the algorithm and this is the minimal spanning tree and its total weight is $(1 + 2 + 3 + 5 + 9) = 20$.
Prim's Algorithm
Prim's algorithm, discovered in 1930 by mathematicians, Vojtech Jarnik and Robert C. Prim, is a greedy algorithm that finds a minimum spanning tree for a connected weighted graph. It finds a tree of that graph which includes every vertex and the total weight of all the edges in the tree is less than or equal to every possible spanning tree. Prims algorithm is faster on dense graphs.
Algorithm
Initialize the minimal spanning tree with a single vertex, randomly chosen from the graph.
Repeat steps 3 and 4 until all the vertices are included in the tree.
Select an edge that connects the tree with a vertex not yet in the tree, so that the weight of the edge is minimal and inclusion of the edge does not form a cycle.
Add the selected edge and the vertex that it connects to the tree.
Problem
Suppose we want to find minimum spanning tree for the following graph G using Prims algorithm.
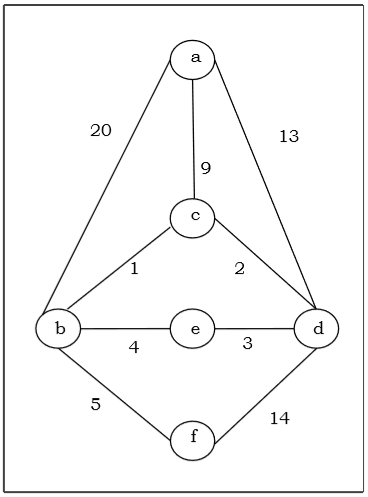
Solution
Here we start with the vertex a and proceed.
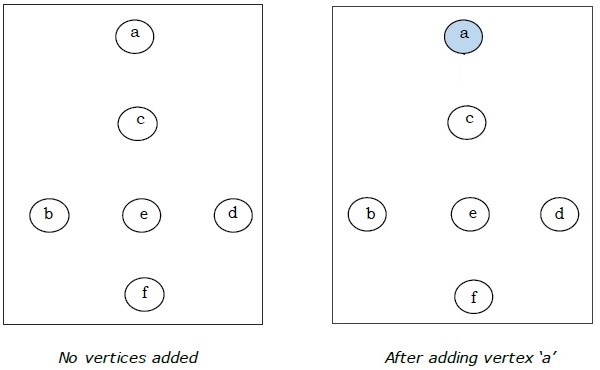
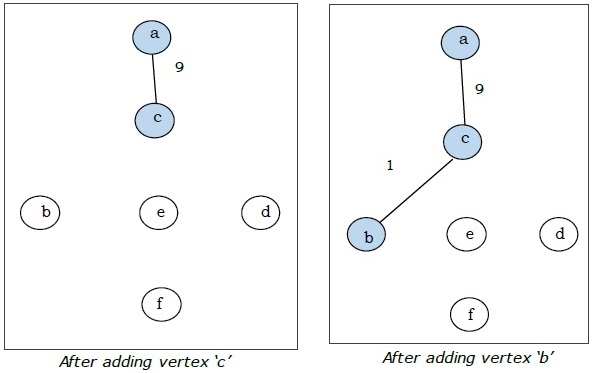
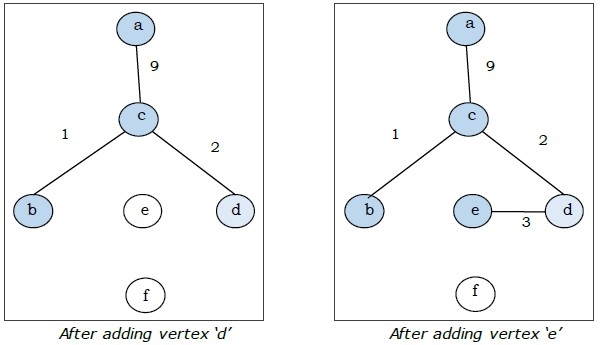
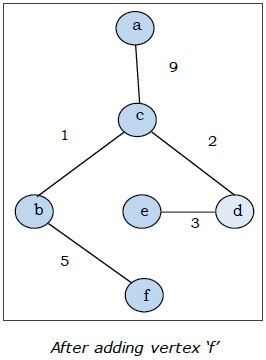
This is the minimal spanning tree and its total weight is $(1 + 2 + 3 + 5 + 9) = 20$.