Image and Inverse-Image in Discrete Mathematics

---

---

Functions are important for mapping elements from one set to another set. As we explore functions more deeply, we find two important concepts: image and inverse-image.

In this chapter, we will elaborate the concept of image and inverse-image with examples for a better understanding. We will show how elements in the domain and codomain of a function are connected.

What are Functions?

Before getting the idea of image and inverse-image, let us see what a function is. A function is a rule that takes elements from one set (called the domain) and maps them to elements in another set (called the codomain). The output that results from applying the function to an element in the domain is called the image of that element.

What is the Image of a Function?

The image of a function is the set of all outputs that the function produces when applied to elements from the domain. More specifically, it is the set of all elements in the codomain that are "hit" or "mapped to" by some element in the domain.

Example of Image

Consider a function f : {1, 2, 3, 4} → {a, b, c} defined as: f(1) = a, f(2) = b, f(3) = a, f(4) = c

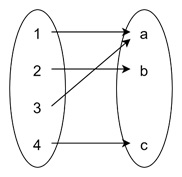
Here, the image of f is the set of all elements in the codomain that are mapped by the function. So in this case, the image is: Image (f) = {a, b, c}

The image includes every codomain element that is assigned to at least one domain element. In our example, every element in the codomain is part of the image because every element of {a, b, c} has at least one input from the domain.

Example of Partial Image

Now, imagine a different function g : {1, 2, 3} → {x, y, z} defined as: g(1) = x, g(2) = y, g(3) = y

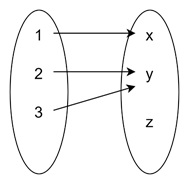
Here, the image is: Image (g) = {x, y}

Notice that z is not part of the image because no element from the domain maps to z. This happens when some elements of the codomain are left "unused."

Subset Image

Another concept of image is the subset image. Concept of image can also apply to a subset of the domain. If we want to know the image of only part of the domain, we can restrict the function to that subset.

Example of Subset Image

Consider the same function f : {1, 2, 3, 4} → {a, b, c}, defined as before. Now, we want to find the image of the subset {1, 4}: Image of {1, 4} = {f(1), f(4)} = {a, c}

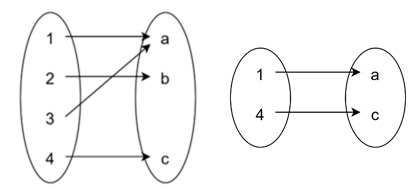
In this case, we are only concerned with the elements in the codomain that correspond to inputs from the subset {1, 4}. The image is simply {a, c}.

Inverse-Image of a Function

Let us now understand the inverse-image (also called the preimage). Given an element in the codomain, which elements in the domain map to it?

Instead of starting with elements from the domain and mapping to the codomain (as with the image), the inverse-image starts with elements in the codomain and traces back to their corresponding elements in the domain.

Example of Inverse-Image

Let us consider the same function f : {1, 2, 3, 4} → {a, b, c} defined as: f(1) = a, f(2) = b, f(3) = a, f(4) = c

Now, suppose we want to find the inverse-image of the element a in the codomain. The inverse-image of a is the set of all elements in the domain that map to a. From the definition of the function, we see that f(1) = a and f(3) = a, so: f⁻¹(a) = {1, 3}

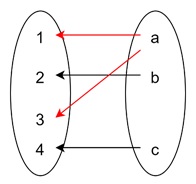
The inverse-image of a includes both 1 and 3, because both of these domain elements map to a.

Empty Inverse-Image

Sometimes, there may be codomain elements that no domain elements map to. In this case, the inverse-image of those elements is the empty set.

For example, if we wanted to find f⁻¹(d) for our function f, we would notice that no domain element maps to d. Therefore, the inverse-image of d is: f⁻¹(d) = ∅

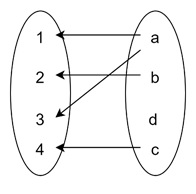
This simply means that d is not mapped by any element from the domain.

Inverse-Image of a Subset

Just like with the image of a subset of the domain, we can also find the inverse-image of a subset of the codomain. In this case, we look for all domain elements that map to any element in the codomain subset.

Example of Inverse-Image of a Subset

Again, using our function f : {1, 2, 3, 4} → {a, b, c}, let us find the inverse-image of the subset {a, c} in the codomain: f⁻¹({a, c}) = {1, 3, 4}

This is because: f(1) = a, f(3) = a, f(4) = c

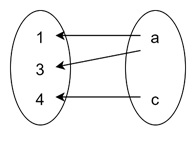
Therefore, the inverse-image of {a, c} includes all domain elements that map to either a or c.

Inverse-Images: Points to Note

The inverse-image of an element in the codomain is always a set, not a single element. This is because multiple domain elements can map to the same codomain element, so the inverse-image might contain more than one element.

The inverse-image only refers to which domain elements map to a given codomain element or set of elements. It is not the same as an inverse function. Inverse functions only exist when the function is a bijection (one-to-one and onto), but inverse-images exist for all types of functions.

Combining Image and Inverse-Image

The concepts of image and inverse-image are closely related, and they are used to understand how a function behaves. The image gives us insight into which codomain elements are "hit" by the function, while the inverse-image tells us where those hits came from in the domain.

In general, the image helps us see the "forward" movement of a function, from the domain to the codomain. The inverse-image allows us to trace backwards, from the codomain to the domain, and identify which domain elements correspond to certain codomain elements.

Conclusion

In this chapter, we explained the concepts of image and inverse-image in the context of functions in discrete mathematics. We have seen that the image is the set of all outputs produced by the function, while the inverse-image helps us find the inputs that lead to certain outputs. We also covered examples where we found both image and inverse-image for individual elements and subsets.