Pascal's Triangle in Discrete Mathematics

---

---

The Pascals Triangle looks very simple at first glance but it has many layers to it. Whether we are counting combinations, working with binomial expansions, or figuring out recursive patterns, the Pascals Triangle helps in making our job easier.

In this chapter, we will explain the basics of Pascals Triangle, understand how it's constructed, and also explore its applications through examples.

What is Pascals Triangle?

The Pascals Triangle is just a triangular pattern of numbers. But what makes it interesting is how each number is built from the two numbers directly above it. The first row starts with a 1 at the top. Each row after that gets wider, and every number in the triangle is the sum of the two numbers above it. If there are no number above, we imagine it as a 0.

Let us see a small version of Pascals Triangle for a basic idea −

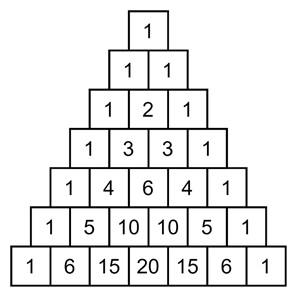
The outer edges of the triangle are always 1. The middle numbers are where things start to get interesting.

Building Pascals Triangle

Making the Pascals Triangle is easy. It follows a certain rule. Start with 1 at the top. In each new number in a row is the sum of the two numbers directly above it. If we are adding a number on the edge of the triangle (where there is only one number above), we treat the "missing" number as a 0.

For example, take the row that starts with 1, 4, 6, 4, 1. How do we get the next row? We add the pairs of numbers directly above −

• 1 + 4 = 5
• 4 + 6 = 10
• 6 + 4 = 10
• 4 + 1 = 5

So, the next row is 1, 5, 10, 10, 5, 1.

Recursive Nature of Pascals Triangle

From the idea of Binomial coefficients, the Pascals Triangle follows a recursive rule. This means each number depends on numbers before it. The recurrence relation for building Pascals Triangle is as follows −

$$\mathrm{\binom{n}{k} \:=\: \binom{n\:-\:1}{k\:-\:1} \:+\: \binom{n\:-\:1}{k}}$$

This is just a special way of saying that each number in the triangle is the sum of the two numbers above it. We can use this relation to find out any number in the triangle if we know the numbers in the row above.

Pascals Triangle and Binomial Coefficients

One of the most important uses of Pascals Triangle is for finding binomial coefficients. These coefficients are the numbers which appear when we expand a binomial expression, like $\mathrm{(x \:+\: y)^n}$. Each row of Pascals Triangle corresponds to the coefficients of a binomial expansion.

For example, the fourth row, 1, 4, 6, 4, 1, gives the coefficients for $\mathrm{(x + y)^4}$

$$\mathrm{(x \:+\: y)^4 \:=\: x^4 \:+\: 4x^3y \:+\: 6x^2y^2 \:+ \:4xy^3 \:+\: y^4}$$

Let us break it down step by step.

Example of Binomial Expansion

Suppose you want to expand $\mathrm{(x + y)^5}$. You can use Pascals Triangle to get the coefficients without doing all the multiplications by hand. The sixth row of the triangle is 1, 5, 10, 10, 5, 1. These are the coefficients −

$$\mathrm{(x \:+\: y)^5 \:=\: x^5 \:+\: 5x^4y \:+\: 10x^3y^2 \:+\: 10x^2y^3 \:+\: 5xy^4 \:+\: y^5}$$

The Pascals Triangle easily help us by saving time to get the coefficients directly. So we do not have to expand the binomial the long way.

Applications of Pascals Triangle

After understanding the basics of Pascals Triangle, let us understand some of the applications of it. It shows up in all kinds of problems, especially when we are using counting problems.

Pascal's Triangle in Combinations

The Pascals Triangle is closely related to combinations. There are ways of choosing items from a set without caring about the order. The numbers in the triangle are exactly the same as the binomial coefficients we use for combinations.

For example, $\mathrm{\binom{5}{2}}$ is the number of ways to choose 2 items from a set of 5. From the triangle, we can see that the number in row 5 and position 2 is 10. So, $\mathrm{\binom{5}{4} \:=\: 10}$, meaning there are 10 ways to choose 2 items from 5.

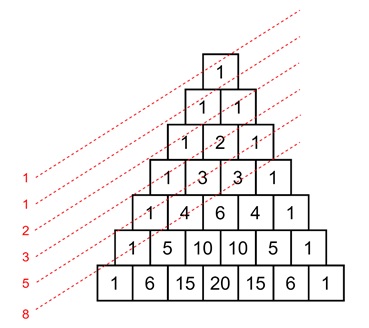
Fibonacci Numbers

Pascals Triangle can also be used to generate Fibonacci numbers. If we add up the numbers along certain diagonals of the triangle, we get Fibonacci numbers. For instance −

• First diagonal: 1
• Second diagonal: 1
• Third diagonal: 1 + 1 = 2
• Fourth diagonal: 1 + 2 = 3
• Fifth diagonal: 1 + 3 + 1 = 5

And so on. These sums give you the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, etc.

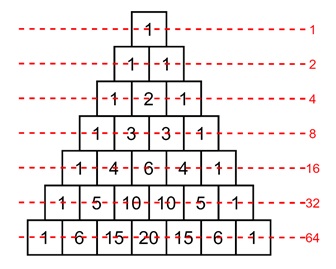
Powers of 2

Another interesting pattern in Pascal's Triangle is that the sum of the numbers in each row gives the powers of 2. If we sum the numbers in the first few rows, you get:

• Row 0: 1 = 2⁰
• Row 1: 1 + 1 = 2¹
• Row 2: 1 + 2 + 1 = 2²
• Row 3: 1 + 3 + 3 + 1 = 2³

This pattern continues as we go down the triangle. It is a quick way to see how powers of 2 grow.

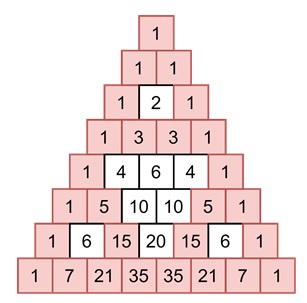
Sierpinskis Triangle

The Pascals Triangle also has a connection to fractals. Specifically the Sierpinski Triangle. If we color in all the odd numbers in Pascals Triangle and leave the even numbers blank, we will start to see a repeating pattern. This pattern is the famous as Sierpinski Triangle, which is a fractal that gets smaller and smaller as we zoom in.

Hidden Patterns in Pascals Triangle

The Pascal's Triangle is full of hidden patterns that might not be visible at first glance. Beyond Fibonacci numbers and powers of 2, there are many other patterns, such as:

• Symmetry − Each row of the triangle is symmetrical. The numbers on the left half mirror the numbers on the right half.
• Triangular numbers − The third diagonal contains the triangular numbers, which represent the number of objects that can form an equilateral triangle. For example, the triangular number 6 represents a triangle with 3 rows, where the bottom row contains 3 objects, the middle row 2, and the top row 1.
• Catalan numbers − These numbers, which show up in combinatorics and computer science, can also be found in Pascal's Triangle with a specific formula with binomial coefficients.

Conclusion

In this chapter, we explained the structure of Pascal's Triangle and its importance in discrete mathematics. We discussed how Pascal's Triangle is constructed and how it relates to binomial expansions.

We highlighted the applications of Pascal's triangle such as combinations, Fibonacci numbers, powers of 2, and even fractals like the Sierpinski Triangle.

Pascal's Triangle is much more than just a triangular arrangement of numbers. It is a useful mathematical tool that provides insight into a wide range of problems, from basic counting to complex recursive relationships.