- Scikit Image – Introduction
- Scikit Image - Image Processing
- Scikit Image - Numpy Images
- Scikit Image - Image datatypes
- Scikit Image - Using Plugins
- Scikit Image - Image Handlings
- Scikit Image - Reading Images
- Scikit Image - Writing Images
- Scikit Image - Displaying Images
- Scikit Image - Image Collections
- Scikit Image - Image Stack
- Scikit Image - Multi Image
- Scikit Image - Data Visualization
- Scikit Image - Using Matplotlib
- Scikit Image - Using Ploty
- Scikit Image - Using Mayavi
- Scikit Image - Using Napari
- Scikit Image - Color Manipulation
- Scikit Image - Alpha Channel
- Scikit Image - Conversion b/w Color & Gray Values
- Scikit Image - Conversion b/w RGB & HSV
- Scikit Image - Conversion to CIE-LAB Color Space
- Scikit Image - Conversion from CIE-LAB Color Space
- Scikit Image - Conversion to luv Color Space
- Scikit Image - Conversion from luv Color Space
- Scikit Image - Image Inversion
- Scikit Image - Painting Images with Labels
- Scikit Image - Contrast & Exposure
- Scikit Image - Contrast
- Scikit Image - Contrast enhancement
- Scikit Image - Exposure
- Scikit Image - Histogram Matching
- Scikit Image - Histogram Equalization
- Scikit Image - Local Histogram Equalization
- Scikit Image - Tinting gray-scale images
- Scikit Image - Image Transformation
- Scikit Image - Scaling an image
- Scikit Image - Rotating an Image
- Scikit Image - Warping an Image
- Scikit Image - Affine Transform
- Scikit Image - Piecewise Affine Transform
- Scikit Image - ProjectiveTransform
- Scikit Image - EuclideanTransform
- Scikit Image - Radon Transform
- Scikit Image - Line Hough Transform
- Scikit Image - Probabilistic Hough Transform
- Scikit Image - Circular Hough Transforms
- Scikit Image - Elliptical Hough Transforms
- Scikit Image - Polynomial Transform
- Scikit Image - Image Pyramids
- Scikit Image - Pyramid Gaussian Transform
- Scikit Image - Pyramid Laplacian Transform
- Scikit Image - Swirl Transform
- Scikit Image - Morphological Operations
- Scikit Image - Erosion
- Scikit Image - Dilation
- Scikit Image - Black & White Tophat Morphologies
- Scikit Image - Convex Hull
- Scikit Image - Generating footprints
- Scikit Image - Isotopic Dilation & Erosion
- Scikit Image - Isotopic Closing & Opening of an Image
- Scikit Image - Skelitonizing an Image
- Scikit Image - Morphological Thinning
- Scikit Image - Masking an image
- Scikit Image - Area Closing & Opening of an Image
- Scikit Image - Diameter Closing & Opening of an Image
- Scikit Image - Morphological reconstruction of an Image
- Scikit Image - Finding local Maxima
- Scikit Image - Finding local Minima
- Scikit Image - Removing Small Holes from an Image
- Scikit Image - Removing Small Objects from an Image
- Scikit Image - Filters
- Scikit Image - Image Filters
- Scikit Image - Median Filter
- Scikit Image - Mean Filters
- Scikit Image - Morphological gray-level Filters
- Scikit Image - Gabor Filter
- Scikit Image - Gaussian Filter
- Scikit Image - Butterworth Filter
- Scikit Image - Frangi Filter
- Scikit Image - Hessian Filter
- Scikit Image - Meijering Neuriteness Filter
- Scikit Image - Sato Filter
- Scikit Image - Sobel Filter
- Scikit Image - Farid Filter
- Scikit Image - Scharr Filter
- Scikit Image - Unsharp Mask Filter
- Scikit Image - Roberts Cross Operator
- Scikit Image - Lapalace Operator
- Scikit Image - Window Functions With Images
- Scikit Image - Thresholding
- Scikit Image - Applying Threshold
- Scikit Image - Otsu Thresholding
- Scikit Image - Local thresholding
- Scikit Image - Hysteresis Thresholding
- Scikit Image - Li thresholding
- Scikit Image - Multi-Otsu Thresholding
- Scikit Image - Niblack and Sauvola Thresholding
- Scikit Image - Restoring Images
- Scikit Image - Rolling-ball Algorithm
- Scikit Image - Denoising an Image
- Scikit Image - Wavelet Denoising
- Scikit Image - Non-local means denoising for preserving textures
- Scikit Image - Calibrating Denoisers Using J-Invariance
- Scikit Image - Total Variation Denoising
- Scikit Image - Shift-invariant wavelet denoising
- Scikit Image - Image Deconvolution
- Scikit Image - Richardson-Lucy Deconvolution
- Scikit Image - Recover the original from a wrapped phase image
- Scikit Image - Image Inpainting
- Scikit Image - Registering Images
- Scikit Image - Image Registration
- Scikit Image - Masked Normalized Cross-Correlation
- Scikit Image - Registration using optical flow
- Scikit Image - Assemble images with simple image stitching
- Scikit Image - Registration using Polar and Log-Polar
- Scikit Image - Feature Detection
- Scikit Image - Dense DAISY Feature Description
- Scikit Image - Histogram of Oriented Gradients
- Scikit Image - Template Matching
- Scikit Image - CENSURE Feature Detector
- Scikit Image - BRIEF Binary Descriptor
- Scikit Image - SIFT Feature Detector and Descriptor Extractor
- Scikit Image - GLCM Texture Features
- Scikit Image - Shape Index
- Scikit Image - Sliding Window Histogram
- Scikit Image - Finding Contour
- Scikit Image - Texture Classification Using Local Binary Pattern
- Scikit Image - Texture Classification Using Multi-Block Local Binary Pattern
- Scikit Image - Active Contour Model
- Scikit Image - Canny Edge Detection
- Scikit Image - Marching Cubes
- Scikit Image - Foerstner Corner Detection
- Scikit Image - Harris Corner Detection
- Scikit Image - Extracting FAST Corners
- Scikit Image - Shi-Tomasi Corner Detection
- Scikit Image - Haar Like Feature Detection
- Scikit Image - Haar Feature detection of coordinates
- Scikit Image - Hessian matrix
- Scikit Image - ORB feature Detection
- Scikit Image - Additional Concepts
- Scikit Image - Render text onto an image
- Scikit Image - Face detection using a cascade classifier
- Scikit Image - Face classification using Haar-like feature descriptor
- Scikit Image - Visual image comparison
- Scikit Image - Exploring Region Properties With Pandas
Scikit Image - Area Closing and Opening an Image
Area closing and area opening are the image processing operations used to manipulate binary or grayscale images based on the size or surface area of objects in the image. Area closing is to remove all dark structures in an image (regions with lower intensity) that have a surface area smaller than a specified threshold, whereas area opening is to remove all bright structures in an image (regions with higher intensity) that have a surface area smaller than a specified threshold.
These operations are particularly useful for tasks such as removing small structures or objects from an image while preserving larger ones.
Scikit-image (skimage) provides the area_closing() and area_opening() functions in the morphology module to perform these operations.
Using the skimage.morphology.area_closing() function
The area_closing() function is used to perform an area closing operation on an input image. Area closing removes dark structures in an image that have a surface (area) smaller than a specified threshold. This operation is similar to morphological closing, but instead of using a fixed structuring element, it employs a deformable one with a surface equal to the area_threshold.
Syntax
Following is the syntax of this function −
skimage.morphology.area_closing(image, area_threshold=64, connectivity=1, parent=None, tree_traverser=None)
Parameters
- image (ndarray): The input image for which the area closing operation is to be performed. This image can be of any type.
- area_threshold (unsigned int): The size parameter, specified in the number of pixels. It defines the minimum surface area that a dark structure must have to be retained. The default value is 64.
- connectivity (unsigned int, optional): The neighborhood connectivity. This parameter specifies the maximum number of orthogonal steps to reach a neighbor. In 2D, it is typically set to 1 for a 4-neighborhood and 2 for an 8-neighborhood. The default value is 1.
- parent (ndarray, int64, optional): A precomputed parent image representing the max tree of the inverted image. Providing a precomputed parent image can speed up the function. This parameter is optional.
- tree_traverser (1D array, int64, optional): A precomputed traverser where the pixels are ordered such that every pixel is preceded by its parent (except for the root, which has no parent). Providing a precomputed traverser can also speed up the function. This parameter is optional.
Return Value
It returns an output image of the same shape and type as the input image, where dark structures with an area smaller than the specified threshold have been removed.
Example
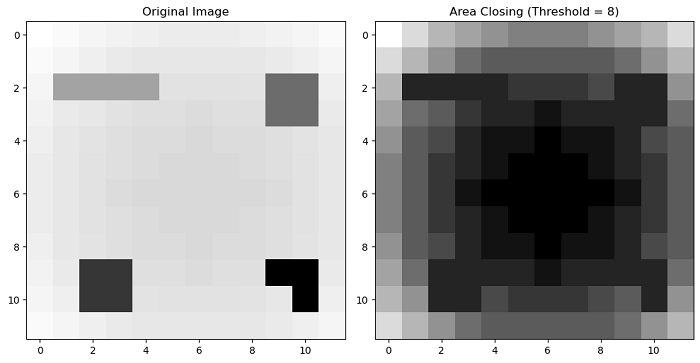
The following example demonstrates how to apply the area_closing() function on an image.
import numpy as np
import matplotlib.pyplot as plt
from skimage.morphology import area_closing
# Create the image
w = 12
x, y = np.mgrid[0:w, 0:w]
image = 180 + 0.2 * ((x - w/2)**2 + (y - w/2)**2)
# Add local minima
image[2:3, 1:5] = 160
image[2:4, 9:11] = 140
image[9:11, 2:4] = 120
image[9:10, 9:11] = 100
image[10, 10] = 100
# Convert the image to integer
image = image.astype(int)
# Perform area closing with a threshold of 8 and connectivity=1
closed = area_closing(image, 8, connectivity=1)
# Display the original and closed images
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
ax = axes.ravel()
ax[0].imshow(image, cmap=plt.cm.gray)
ax[0].set_title('Original Image')
ax[1].imshow(closed, cmap=plt.cm.gray)
ax[1].set_title('Area Closing (Threshold = 8)')
plt.tight_layout()
plt.show()
Output
On executing the above program, you will get the following output −
Using the skimage.morphology.area_opening() function
The area_opening() function is used to perform an area opening operation on an input image. Area opening removes bright structures in an image that have a surface area smaller than a specified threshold. This operation is similar to the morphological opening, but instead of using a fixed structuring element, it employs a deformable one with a surface area equal to the area_threshold.
Syntax
Following is the syntax of this function −
skimage.morphology.area_opening(image, area_threshold=64, connectivity=1, parent=None, tree_traverser=None)
Parameters
- image (ndarray): The input image for which the area opening operation is to be performed. This image can be of any type.
- area_threshold (unsigned int): The size parameter, specified in the number of pixels. The default value is set to 64, but you can adjust it as needed.
- connectivity (unsigned int, optional): The neighborhood connectivity. This parameter specifies the maximum number of orthogonal steps to reach a neighbor. In 2D, it is typically set to 1 for a 4-neighborhood and 2 for an 8-neighborhood. The default value is 1.
- parent (ndarray, int64, optional): A precomputed parent image representing the max tree of the image. The value of each pixel is the index of its parent in the ravelled array.
- tree_traverser (1D array, int64, optional): A precomputed traverser where the pixels are ordered such that every pixel is preceded by its parent (except for the root, which has no parent).
Return Value
It returns an output image of the same shape and type as the input image, where bright structures with a surface area smaller than the specified threshold have been removed.
Example
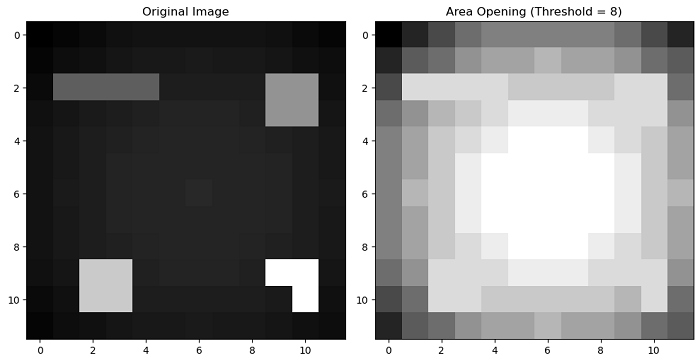
In the following example, we create a quadratic function with a maximum in the center and add four additional local maxima to simulate a multi-peak image. Then the area_opening() function is applied with a threshold of 8, which means that bright peaks with a surface area smaller than 8 pixels will be removed.
import numpy as np
import matplotlib.pyplot as plt
from skimage.morphology import area_opening
# Create the image
w = 12
x, y = np.mgrid[0:w, 0:w]
image = 20 - 0.2 * ((x - w/2)**2 + (y - w/2)**2)
# Add local maxima
image[2:3, 1:5] = 40
image[2:4, 9:11] = 60
image[9:11, 2:4] = 80
image[9:10, 9:11] = 100
image[10, 10] = 100
# Convert the image to integer
image = image.astype(int)
# Perform area opening with a threshold of 8 and connectivity=1
opened = area_opening(image, 8, connectivity=1)
# Display the original and closed images
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
ax = axes.ravel()
ax[0].imshow(image, cmap=plt.cm.gray)
ax[0].set_title('Original Image')
ax[1].imshow(opened, cmap=plt.cm.gray)
ax[1].set_title('Area Opening (Threshold = 8)')
plt.tight_layout()
plt.show()
Output
On executing the above program, you will get the following output −