Scikit Image - Probabilistic Hough Transform

Previous
Quiz
Next

The Probabilistic Hough Transform is a technique used in image analysis and computer vision to detect shapes, patterns, or structures in an image. Unlike the traditional Hough Transform, which accumulates all possible configurations of a shape.

The Probabilistic Hough Transform adopts a more efficient approach by sampling a random subset of voting points. This method approximates the final outcome effectively and allows the extraction of lines during the voting process by tracing along connected components. This returns the start and end points of each line segment, which is a valuable output.

Pythons, scikit-image library provides a function probabilistic_hough_line() in the transform module to perform the Probabilistic Hough Transform on images.

Using the skimage.transform.probabilistic_hough_line() function

The transform.probabilistic_hough_line() function is used to perform a progressive probabilistic line Hough transform on an input image containing edges.

Syntax

Following is the syntax of this function −

skimage.transform.probabilistic_hough_line(image, threshold=10, line_length=50, line_gap=10, theta=None, rng=None)

Parameters

  • image: The input image with nonzero values representing edges.
  • threshold: An optional integer parameter that sets the threshold.
  • line_length: An optional parameter that defines the minimum length of detected lines. Increasing this parameter extracts longer line segments.
  • line_gap: An optional parameter that sets the maximum gap allowed between pixels to still form a line. Increasing this parameter can help merge broken or interrupted lines.
  • theta: An optional parameter that specifies the angles at which to compute the Hough transform. It is a 1D NumPy array of double values representing angles in radians. By default, it generates a vector of 180 angles evenly spaced in the range from -pi/2 to pi/2.
  • rng: An optional parameter that allows you to specify a pseudo-random number generator (RNG) for probabilistic aspects of the algorithm. It can be a numpy.random.Generator instance or an integer seed. By default, a PCG64 generator is used.

Return Value

It returns a list of detected lines, where each line is represented as a tuple of two points: ((x0, y0), (x1, y1)), indicating the start and end points of the line in the image.

Example

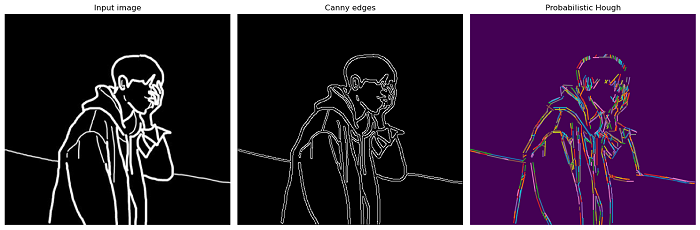
The following example demonstrates how to use the probabilistic_hough_line() function to detect and highlight detected lines in an image.

import numpy as np
import matplotlib.pyplot as plt
from skimage.transform import probabilistic_hough_line
from skimage.feature import canny
from skimage import io, color

# Load an input image
image = io.imread('Images/Road.jpg', as_gray=True)

# Apply Canny edge detection
edges = canny(image)

# Define the Angles for which to calculate the transform
tested_angles = np.linspace(-np.pi / 2, np.pi / 2, 360, endpoint=False)

# Apply probabilistic Hough line transform
lines = probabilistic_hough_line(edges,  threshold=5, line_length=10, line_gap=3, theta=tested_angles)

# Display the results
fig, axes = plt.subplots(1, 3, figsize=(15, 5), sharex=True, sharey=True)

axes[0].imshow(image, cmap='gray')
axes[0].set_title('Input image')
axes[0].axis('off')

axes[1].imshow(edges, cmap='gray')
axes[1].set_title('Canny edges')
axes[1].axis('off')

axes[2].imshow(edges * 0)
for line in lines:
    p0, p1 = line
    axes[2].plot((p0[0], p1[0]), (p0[1], p1[1]))
axes[2].set_xlim((0, image.shape[1]))
axes[2].set_ylim((image.shape[0], 0))
axes[2].set_title('Probabilistic Hough')
axes[2].axis('off')

plt.tight_layout()
plt.show()

Output

On executing the above program, you will get the following output −

Example

The following example demonstrates how to use the probabilistic_hough_line() function to detect lines in an image by specifying the angles(theta) for which to calculate the transform.

import numpy as np
import matplotlib.pyplot as plt
from skimage.transform import probabilistic_hough_line
from skimage.feature import canny
from skimage import io

# Load an input image
image = io.imread('Images/Road.jpg', as_gray=True)

# Apply Canny edge detection
edges = canny(image)

# Define the Angles for which to calculate the transform
tested_angles = np.linspace(-np.pi / 2, np.pi / 2, 360, endpoint=False)

# Apply probabilistic Hough line transform
lines = probabilistic_hough_line(edges,  threshold=5, line_length=10, line_gap=3, theta=tested_angles)

# Display the results
fig, axes = plt.subplots(1, 3, figsize=(15, 5), sharex=True, sharey=True)

axes[0].imshow(image, cmap='gray')
axes[0].set_title('Input image')
axes[0].axis('off')

axes[1].imshow(edges, cmap='gray')
axes[1].set_title('Canny edges')
axes[1].axis('off')

axes[2].imshow(edges * 0)
for line in lines:
    p0, p1 = line
    axes[2].plot((p0[0], p1[0]), (p0[1], p1[1]))
axes[2].set_xlim((0, image.shape[1]))
axes[2].set_ylim((image.shape[0], 0))
axes[2].set_title('Probabilistic Hough')
axes[2].axis('off')

plt.tight_layout()
plt.show()

Output

On executing the above program, you will get the following output −

Print Page
Previous
Next
Advertisements