
- Computer Graphics - Home
- Computer Graphics Basics
- Computer Graphics Applications
- Graphics APIs and Pipelines
- Computer Graphics Maths
- Sets and Mapping
- Solving Quadratic Equations
- Computer Graphics Trigonometry
- Computer Graphics Vectors
- Linear Interpolation
- Computer Graphics Devices
- Cathode Ray Tube
- Raster Scan Display
- Random Scan Device
- Phosphorescence Color CRT
- Flat Panel Displays
- 3D Viewing Devices
- Images Pixels and Geometry
- Color Models
- Line Generation
- Line Generation Algorithm
- DDA Algorithm
- Bresenham's Line Generation Algorithm
- Mid-point Line Generation Algorithm
- Circle Generation
- Circle Generation Algorithm
- Bresenham's Circle Generation Algorithm
- Mid-point Circle Generation Algorithm
- Ellipse Generation Algorithm
- Polygon Filling
- Polygon Filling Algorithm
- Scan Line Algorithm
- Flood Filling Algorithm
- Boundary Fill Algorithm
- 4 and 8 Connected Polygon
- Inside Outside Test
- 2D Transformation
- 2D Transformation
- Transformation Between Coordinate System
- Affine Transformation
- Raster Methods Transformation
- 2D Viewing
- Viewing Pipeline and Reference Frame
- Window Viewport Coordinate Transformation
- Viewing & Clipping
- Point Clipping Algorithm
- Cohen-Sutherland Line Clipping
- Cyrus-Beck Line Clipping Algorithm
- Polygon Clipping Sutherland–Hodgman Algorithm
- Text Clipping
- Clipping Techniques
- Bitmap Graphics
- 3D Viewing Transformation
- 3D Computer Graphics
- Parallel Projection
- Orthographic Projection
- Oblique Projection
- Perspective Projection
- 3D Transformation
- Rotation with Quaternions
- Modelling and Coordinate Systems
- Back-face Culling
- Lighting in 3D Graphics
- Shadowing in 3D Graphics
- 3D Object Representation
- Represnting Polygons
- Computer Graphics Surfaces
- Visible Surface Detection
- 3D Objects Representation
- Computer Graphics Curves
- Computer Graphics Curves
- Types of Curves
- Bezier Curves and Surfaces
- B-Spline Curves and Surfaces
- Data Structures For Graphics
- Triangle Meshes
- Scene Graphs
- Spatial Data Structure
- Binary Space Partitioning
- Tiling Multidimensional Arrays
- Color Theory
- Colorimetry
- Chromatic Adaptation
- Color Appearance
- Antialiasing
- Ray Tracing
- Ray Tracing Algorithm
- Perspective Ray Tracing
- Computing Viewing Rays
- Ray-Object Intersection
- Shading in Ray Tracing
- Transparency and Refraction
- Constructive Solid Geometry
- Texture Mapping
- Texture Values
- Texture Coordinate Function
- Antialiasing Texture Lookups
- Procedural 3D Textures
- Reflection Models
- Real-World Materials
- Implementing Reflection Models
- Specular Reflection Models
- Smooth-Layered Model
- Rough-Layered Model
- Surface Shading
- Diffuse Shading
- Phong Shading
- Artistic Shading
- Computer Animation
- Computer Animation
- Keyframe Animation
- Morphing Animation
- Motion Path Animation
- Deformation Animation
- Character Animation
- Physics-Based Animation
- Procedural Animation Techniques
- Computer Graphics Fractals
Bresenham's Circle Generation Algorithm
Bresenham's Circle Generation Algorithm is a fundamental technique in computer graphics to generate circles. In this chapter, we will explain how the algorithm works, its steps, and provide a detailed example, for a better understanding.
Bresenham's Circle Generation Algorithm
Bresenham's algorithm for circles works by generating points from 90 to 45. It makes moves only in the +X and -Y directions. The goal is to find the pixels that best approximate a true circle on a digital screen.
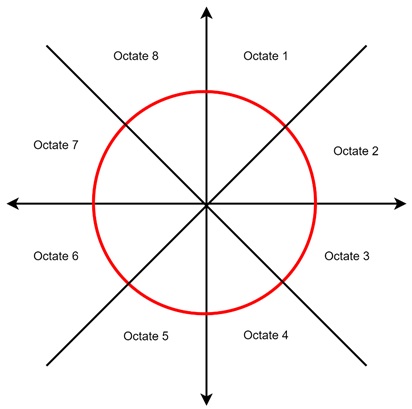
How does the Bresenham's Circle Generation Algorithm Works?
Let's understand how the Bresenham's circle generation algorithm works −
- Point Generation − The algorithm starts at 90° and moves towards 45°. It decides which pixel to light up next based on two possible actions:
- Move one unit in the x-direction − Move one unit in both the x-direction and negative y-direction
- Decision VariableTo choose between these actions, the algorithm uses a decision variable 'd'. This variable helps determine which pixel is closest to the true circle.
- Eight-Way Symmetry − The algorithm uses eight-way symmetry. This means it only calculates points for one octant of the circle, as given in the above figure for the octates. Then it reflects these points to create the full circle.
Algorithm Steps
Here is a step-by-step breakdown of Bresenham's Circle Algorithm −
Step 1 − Start the algorithm
Step 2 − Declare variables: p, q (circle centre coordinates), x, y (current point), r (radius), d (decision variable)
Step 3 − Input the radius r
Step 4 − Calculate initial d: d = 3 - 2r
Step 5 − Set initial x = 0, y = r
Step 6 − Check if x y. If true, stop. If false, continue
Step 7 − Plot eight symmetric points
Step 8 − Update d and x (and y if needed)
Step 9 − Go back to step 6
Step 10 − End the algorithm
Example
For centre at point (0, 0) with radius 10, the algorithm will work in the following way −
| Step | x | y | d | Symmetric Points |
|---|---|---|---|---|
| Init | 0 | 10 | d = 3 - 2 * r = -17 | (0, 10), (0, -10), (10, 0), (-10, 0) |
| 1 | 1 | 10 | d + 4 * x + 6 = -17 + 4 = -13 | (1, 10), (1, -10), (-1, -10), (-1, 10), (10, 1), (10, -1), (-10, -1), (-10, 1) |
| 2 | 2 | 10 | d + 4 * x + 6 = -13 + 4 = -9 | (2, 10), (2, -10), (-2, -10), (-2, 10), (10, 2), (10, -2), (-10, -2), (-10, 2) |
| 3 | 3 | 10 | d + 4 * x + 6 = -9 + 4 = -5 | (3, 10), (3, -10), (-3, -10), (-3, 10), (10, 3), (10, -3), (-10, -3), (-10, 3) |
| 4 | 4 | 9 | d + 4 * x - 4 * y + 10 = -5 + 4 - 8 + 10 = 1 | (4, 9), (4, -9), (-4, -9), (-4, 9), (9, 4), (9, -4), (-9, -4), (-9, 4) |
| 5 | 5 | 9 | d - 4 * y + 10 = 1 - 8 + 10 = 3 | (5, 9), (5, -9), (-5, -9), (-5, 9), (9, 5), (9, -5), (-9, -5), (-9, 5) |
| 6 | 6 | 8 | d + 4 * x - 4 * y + 10 = 3 + 4 - 8 + 10 = 9 | (6, 8), (6, -8), (-6, -8), (-6, 8), (8, 6), (8, -6), (-8, -6), (-8, 6) |
| 7 | 7 | 7 | d + 4 * x - 4 * y + 10 = 9 + 4 - 8 + 10 = 15 | (7, 7), (7, -7), (-7, -7), (-7, 7) |
x = 0, y = r = 10 is the starting point, and the decision variable d is initialized. For each step, the decision variable d is updated. If d <= 0, only x is incremented; otherwise, both x and y are updated.
At each step, the 8-way symmetric points are calculated and printed as shown in the table. The resulting coordinates will draw the circle with the centre at (0, 0) and radius 10.
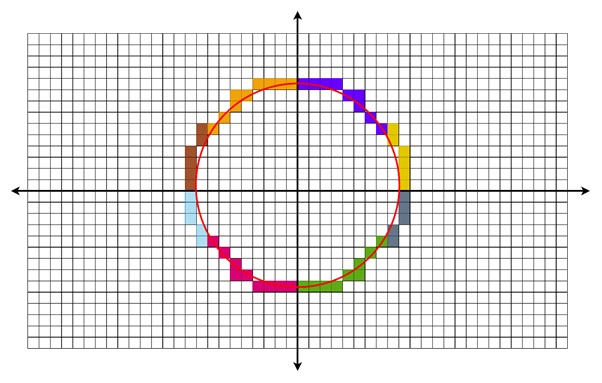
Advantages of Bresenham's Circle Generation Algorithm
Bresenham's Circle Generation Algorithm has several benefits, it uses only integer addition and subtraction which is efficient. And this makes it faster than other circle-drawing methods. It produces circles that closely approximate true circles.
Conclusion
In this chapter, we explained the Bresenham's Circle Generation Algorithm in detail. We covered its basic concept, how it works, and provided a step-by-step breakdown of the algorithm. We also walked through a detailed example.
In the next chapter, we will see another circle generation algorithm called the mid-point algorithm which is quite similar to Bresenham's algorithm.