Procedural Techniques for Animation in Computer Graphics

---

---

Unlike manual methods such as keyframing or physics-based animation, procedural techniques use algorithms or mathematical functions to create movements and effects. Procedural techniques help in creating complex, dynamic animations with less human input. It is useful while depicting natural phenomena like waves, clouds, or random patterns.

In this chapter, we will explain the fundamentals of procedural techniques in computer animation, discuss their applications, and provide examples for a better understanding.

Basics of Procedural Techniques for Animation

Procedural animation is about generating motion or patterns using a predefined set of rules or mathematical functions. These functions can be used to mimic natural processes or other complex phenomena.

One of the most well-known procedural techniques is noise-based animation, where random or semi-random values are used to create patterns that evolve over time.

Procedural animations are used in situations where realism is important but manually animating each frame would be too time-consuming. For example, animating the surface of a lake with waves can be done procedurally by applying mathematical formulas that simulate the movement of water. Rather than keyframing every wave, a simple function can be used to automatically generate the desired effect.

Waves and Simple Motion

One of the simplest examples of procedural animation is creating a constant wave pattern, such as the movement of water. This can be done using a formula that describes a wave’s motion over time and space.

For instance, the following function can create a simple wave −

$$\mathrm{f(x,\: t) \:=\: A \:\cdot\: \cos (\omega\: t \:-\: kx \:+\: \varphi)}$$

Here, A is the amplitude of the wave, ω is the frequency, k is the wave vector, is the phase, and x and t represent position and time. By changing these parameters, animators can control the appearance and speed of the waves.

Let us see this animation in action −

Procedural Noise

Procedural animation uses noise to make more realistic nature of animations. Noise functions generate random or pseudo-random values that can be used to create textures, clouds, or terrain in both 2D and 3D spaces. The most well-known noise function is Perlin noise, which produces smooth, natural-looking random patterns.

By animating the parameters of a noise function over time, animators can create effects like moving clouds or turbulent water. For instance, to animate a noise-based pattern, the following simple technique can be applied −

$$\mathrm{\text{timenoise }(x,\: t) \:=\: \text{noise }(x \:+\: vt)}$$

This equation moves the pattern through space at a constant speed, v, by modifying the input values of the noise function over time. More complex motions, such as spirals or random trajectories, can also be applied by adjusting the function’s parameters in more sophisticated ways.

Noise functions are particularly useful in animation because they give a high level of control while still maintaining an organic, unpredictable look. This is ideal for simulating natural elements like clouds, fire, or flowing water, where complete randomness would appear unrealistic, but structured motion would look too artificial.

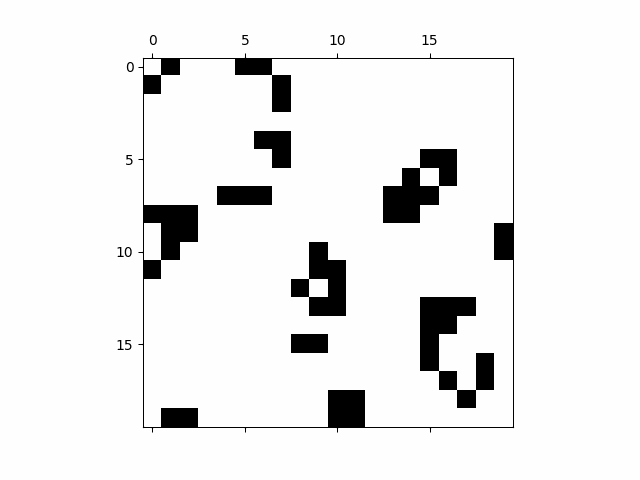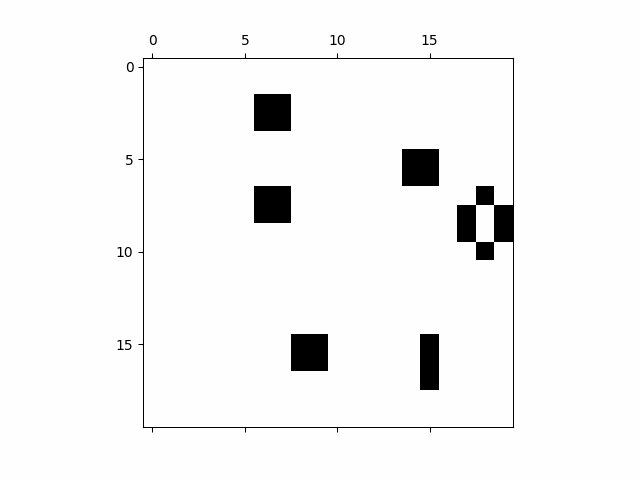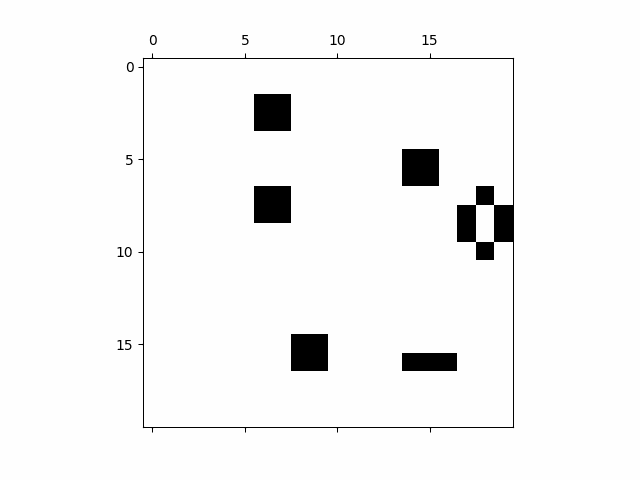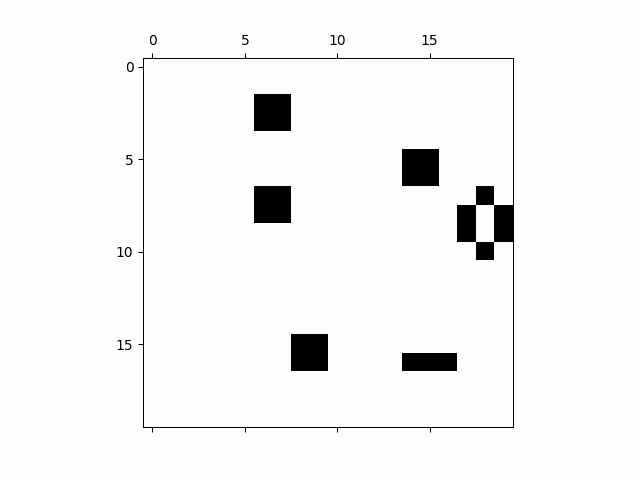
Cellular Automata

Another interesting procedural technique is cellular automata. A cellular automaton is a grid of cells, each of which can be in a different state (e.g., alive or dead). The state of each cell changes over time based on a set of predefined rules, often influenced by the states of neighboring cells.

The best-known example of cellular automata is the Game of Life, created by British mathematician John Conway in 1970.

The rules for Conway's Game of Life are simple −

• A dead cell with exactly three live neighbours becomes a live cell.
• A live cell with two or three live neighbours stays alive.
• In all other cases, the cell dies or remains dead.

By applying these rules repeatedly over time, complex patterns and behaviors can emerge from very simple initial conditions. In animation, cellular automata can be used to create organic-looking effects such as growing patterns, fire, or even cloud formation.

L-Systems

L-systems, short for Lindenmayer systems, are used for simulating plant growth patterns. Originally developed by biologist Aristid Lindenmayer, they consist of recursive rules that generate complex structures from simple instructions.

The system has expanding a starting string of symbols to generate a more complex string, each symbol corresponding to a geometric command. The final string is then interpreted as instructions to create a plant-like structure.

For example, a simple L-system rule might look like this −

$$\mathrm{S \:\rightarrow\: A}$$

$$\mathrm{A \:\rightarrow\: [+B]fA}$$

$$\mathrm{B \:\rightarrow\: fB}$$

In this case, the symbol S starts the process, A and B represent branches, and the commands such as "f", "+", and "[" these are used to control the position and orientation of the branches. By repeatedly applying these rules, complex plant structures can be generated.

L-systems are particularly effective for creating trees, bushes, and other organic structures because they mimic the branching patterns found in nature. Additionally, L-systems can simulate growth over time by gradually applying the rules, making it an ideal technique for animating the natural development of plants.

Advantages of Procedural Techniques

Let us see the advantages of these kind of animations. One of the main advantages of procedural techniques is their ability to create complex and dynamic animations without requiring extensive manual input. By defining a set of rules or functions, animators can generate motion and patterns that would be difficult or impossible to achieve through traditional keyframing techniques.

Another benefit is the efficiency of procedural techniques. Since the computer is responsible for calculating the motion based on the rules provided, these methods can save a lot of time in the animation process. This is especially useful for large-scale simulations, such as animating crowds, landscapes, or natural phenomena.

Challenges in Procedural Techniques

One of the biggest challenges in procedural techniques is that they can be hard to control. Since the motion or patterns are generated algorithmically, the animator has less direct control over the exact outcome. This can make it difficult to achieve precise movements or specific visual effects without extensive tweaking of the parameters.

Another challenge is the complexity of designing the procedural rules or functions. For example, creating an L-system that accurately mimics the growth of a tree requires a deep understanding of both the underlying biological processes and the mechanics of the L-system itself. Similarly, designing noise functions or cellular automata that produce realistic results can be a time-consuming process.

Conclusion

In this chapter, we explained the concept of procedural techniques for animation in computer graphics. We started by discussing the basics of procedural animation. That is, using algorithms and mathematical functions to generate motion and patterns automatically. We presented specific examples such as wave simulation, cellular automata, and discussed on L-systems, which are widely used to simulate natural phenomena and organic growth patterns.

We also covered the advantages of procedural techniques, including their efficiency, flexibility, and ability to create complex animations with minimal manual input. Finally, we highlighted some of the challenges associated with procedural methods, such as the difficulty of controlling the outcome and the complexity of designing the underlying rules.