
- Computer Graphics - Home
- Computer Graphics Basics
- Computer Graphics Applications
- Graphics APIs and Pipelines
- Computer Graphics Maths
- Sets and Mapping
- Solving Quadratic Equations
- Computer Graphics Trigonometry
- Computer Graphics Vectors
- Linear Interpolation
- Computer Graphics Devices
- Cathode Ray Tube
- Raster Scan Display
- Random Scan Device
- Phosphorescence Color CRT
- Flat Panel Displays
- 3D Viewing Devices
- Images Pixels and Geometry
- Color Models
- Line Generation
- Line Generation Algorithm
- DDA Algorithm
- Bresenham's Line Generation Algorithm
- Mid-point Line Generation Algorithm
- Circle Generation
- Circle Generation Algorithm
- Bresenham's Circle Generation Algorithm
- Mid-point Circle Generation Algorithm
- Ellipse Generation Algorithm
- Polygon Filling
- Polygon Filling Algorithm
- Scan Line Algorithm
- Flood Filling Algorithm
- Boundary Fill Algorithm
- 4 and 8 Connected Polygon
- Inside Outside Test
- 2D Transformation
- 2D Transformation
- Transformation Between Coordinate System
- Affine Transformation
- Raster Methods Transformation
- 2D Viewing
- Viewing Pipeline and Reference Frame
- Window Viewport Coordinate Transformation
- Viewing & Clipping
- Point Clipping Algorithm
- Cohen-Sutherland Line Clipping
- Cyrus-Beck Line Clipping Algorithm
- Polygon Clipping Sutherland–Hodgman Algorithm
- Text Clipping
- Clipping Techniques
- Bitmap Graphics
- 3D Viewing Transformation
- 3D Computer Graphics
- Parallel Projection
- Orthographic Projection
- Oblique Projection
- Perspective Projection
- 3D Transformation
- Rotation with Quaternions
- Modelling and Coordinate Systems
- Back-face Culling
- Lighting in 3D Graphics
- Shadowing in 3D Graphics
- 3D Object Representation
- Represnting Polygons
- Computer Graphics Surfaces
- Visible Surface Detection
- 3D Objects Representation
- Computer Graphics Curves
- Computer Graphics Curves
- Types of Curves
- Bezier Curves and Surfaces
- B-Spline Curves and Surfaces
- Data Structures For Graphics
- Triangle Meshes
- Scene Graphs
- Spatial Data Structure
- Binary Space Partitioning
- Tiling Multidimensional Arrays
- Color Theory
- Colorimetry
- Chromatic Adaptation
- Color Appearance
- Antialiasing
- Ray Tracing
- Ray Tracing Algorithm
- Perspective Ray Tracing
- Computing Viewing Rays
- Ray-Object Intersection
- Shading in Ray Tracing
- Transparency and Refraction
- Constructive Solid Geometry
- Texture Mapping
- Texture Values
- Texture Coordinate Function
- Antialiasing Texture Lookups
- Procedural 3D Textures
- Reflection Models
- Real-World Materials
- Implementing Reflection Models
- Specular Reflection Models
- Smooth-Layered Model
- Rough-Layered Model
- Surface Shading
- Diffuse Shading
- Phong Shading
- Artistic Shading
- Computer Animation
- Computer Animation
- Keyframe Animation
- Morphing Animation
- Motion Path Animation
- Deformation Animation
- Character Animation
- Physics-Based Animation
- Procedural Animation Techniques
- Computer Graphics Fractals
Boundary Fill Algorithm in Computer Graphics
The Boundary Fill algorithm works by starting from a point inside the polygon and spreading outwards until the boundaries are reached. In this chapter, we will explain the basics of Boundary Fill algorithm and how it is applied in Polygon Filling. We will also go through a step-by-step example for a better understanding.
Boundary Fill Algorithm
The boundary filling algorithm is applied for filling an area of connected pixels with a specific color other than the boundary color. It requires boundary of same color. It fills all the connected areas until it reaches a boundary.
The algorithm starts from a point (usually inside the area to be filled) and changes the color of all adjacent pixels that match the starting pixel.
In polygon filling, the goal is to color the inside of a polygon. It assumes the boundary color are different and it remain intact.
Key Features of Boundary Filling Algorithm
Let us see some of the components of boundary filling algorithms.
- Seed Point − This is the starting point inside the polygon where the filling process begins, it can be any point inside the polygon.
- Boundary Condition − The algorithm stops when it reaches the edges or boundaries of the polygon. Boundaries must have different color than the filling color.
- Recursion or Stack-Based − The algorithm can be implemented recursively or using an explicit stack to avoid deep recursion issues.
Types of Boundary Fill Algorithms
There are two types of filling, depending on the specific requirement −
- 4-Connected boundary filling − Fills pixels connected horizontally or vertically to the seed point.
- 8-Connected boundary filling − Fills pixels connected diagonally, horizontally, and vertically.
How Does the Boundary Fill Algorithm Work?
The boundary fill algorithm operates by checking the color of each neighbouring pixel. If the color of the pixel matches the target color, it gets filled with a new color, and the algorithm proceeds to its neighbours. The process continues until all the pixels inside the boundary are filled.
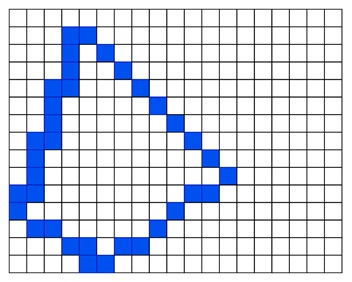
Let us see the example of how 4-connected boundary filling is working with. Initially we have a polygon with blue boundary.
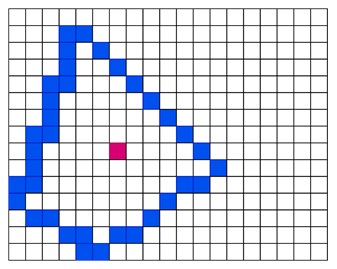
Now, pick a seed at center and its color is red.
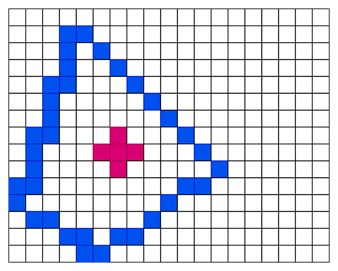
After that, it will expand using 4-connected pixels and nearest 4 pixels are turned red.
Then again, the 4 connected pixels of the newly colored pixels will be turned red but here all pixels which are colored before will not be affected.
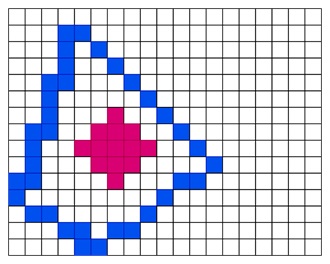
And finally, it will be filled like below −
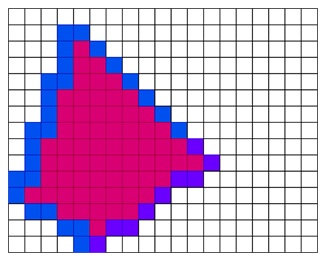
This is how the Boundary Fill Algorithm works. The basic logic of boundary fill can be explained in three steps −
- Pick a Seed Point − Start with a pixel inside the polygon.
- Check Adjacent Pixels − Look at the neighboring pixels and determine if they should be filled.
- Fill the Pixel − If the pixel is part of the interior, fill it with the desired color and move to the next.
The algorithm works recursively, so that it calls itself for each neighbouring pixel that needs to be filled. However, recursion can sometimes lead to stack overflow in large areas. To avoid this, an iterative version using a stack can be employed.
Recursive Algorithm
Let us see the recursive algorithm −
Function BoundaryFill(x, y, targetColor, fillColor):
If (pixel at (x, y) is not targetColor or is already fillColor) then
Return
Set pixel at (x, y) to fillColor
BoundaryFill(x+1, y, targetColor, fillColor) // Right
BoundaryFill(x-1, y, targetColor, fillColor) // Left
BoundaryFill(x, y+1, targetColor, fillColor) // Down
BoundaryFill(x, y-1, targetColor, fillColor) // Up
Also, see the iterative approach −
Function BoundaryFill(x, y, targetColor, fillColor):
Create an empty stack
Push (x, y) onto the stack
While the stack is not empty:
Pop (currentX, currentY) from the stack
If (pixel at (currentX, currentY) is targetColor):
Set pixel at (currentX, currentY) to fillColor
Push neighbors of (currentX, currentY) onto the stack
Advantages and Disadvantages of Boundary Fill Algorithm
The boundary fill algorithm is easy to understand and simple to implement. It can handle polygons with complex and irregular shapes, as long as the boundaries are well-defined.
On the downside, the boundary fill algorithm can be slow for large polygons, especially in the recursive version, which might cause stack overflow. The fill is uncontrolled beyond the boundary condition, so filling precision is determined by the boundary's accuracy.
Difference between Flood-fill and Boundary-fill Algorithm
The following table highlights the major differences between Flood-Fill Algorithm and Boundary-Fill Algorithm −
| Flood-fill Algorithm | Boundary-fill Algorithm |
|---|---|
| Can handle multiple boundary colors | Can only process single boundary colors |
| Slower than the boundary-fill algorithm | Faster than the flood-fill algorithm |
| Uses random color to fill the interior area | Fills the interior area by checking the boundary color |
| Requires more memory | Requires less memory |
| Simple and efficient for complex shapes | More complex than the flood-fill algorithm |
Conclusion
In this chapter, we explained how the Boundary Fill Algorithm is applied to fill the interior of polygons. We also covered their types, the process it follows, and the difference between recursive and iterative implementations. We also provided an illustrative example where we picked a polygon and filled it using the 4-connected polygon filling approach to understand the concept in a clear way.