Images, Pixels and Geometry in Computer Graphics

---

---

Pixels are the building blocks of images. In digital images, there is a complex relationship between pixels, geometry, and mathematical principles. Read this chapter to understand the foundational concepts of images, pixels, and geometry in computer graphics.

Concept of Digital Image

As we all know, a digital image is a two-dimensional representation of visual information. While working with graphics, images are backbone of it. Images are formed by tiny units called pixels. The word "pixel" is short for "picture element".

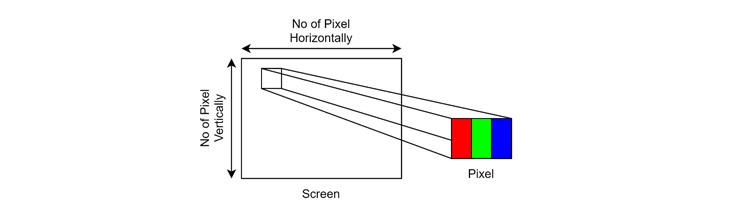
When viewed closely, pixels appear as tiny squares or dots, but when viewed from a distance, they blend to form smooth, cohesive images.

Pixels and Resolution

Pixels are arranged in a grid, and the number of pixels in an image determines its called the resolution. A higher resolution means more pixels in a small area thus detailed images are formed. For instance, an image with a resolution of 1920x1080 pixels (Full HD) has 2,073,600 individual pixels.

The quality and clarity of an image largely depend on its resolution. In digital displays, this translates to the number of pixels on the screen. An image with a low resolution may appear blurry or pixelated when magnified.

Color Depth and Pixel Information

Each pixel in a digital image stores information about its color and brightness. This is achieved through the concept of color depth. The color depth refers to the number of bits used to represent a pixel's color. A common example is 24-bit color, where 8 bits each are used for red, green, and blue channels. So this is nearly 16.7 million possible color combinations.

The Geometry of Computer Graphics

Sometimes we can make vector graphics with equations. In this case we need to consider the geometry. Geometry involves the shapes, positions, and transformations in space, whether it be two-dimensional or three-dimensional.

2D Geometry

In two-dimensional (2D) computer graphics, geometric shapes such as lines, circles, and polygons are defined using coordinate systems. Each point in the image is represented by a pair of coordinates (x, y) that correspond to its position on the screen or image canvas.

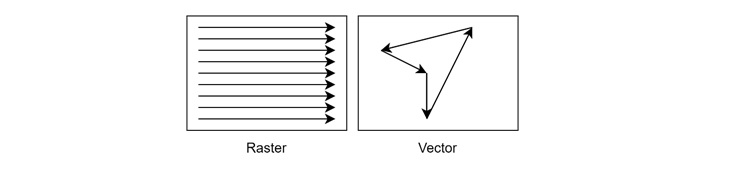
Vector graphics, a type of 2D representation, use geometric primitives (points, lines, curves, etc.) to define images. Unlike raster images, which are pixel-based, vector graphics maintain their quality when scaled up or down.

Transformations like translation (moving), rotation, and scaling can be applied to these shapes using mathematical operations, often represented as matrices.

3D Geometry

For 3D space, computer graphics is more complex, involving not only the x and y coordinates but also the z-axis to represent depth. This allows for the creation of objects that exist in a simulated 3D space, which can be viewed from different angles.

3D Transformations and Projections

Just as with 2D graphics, transformations can be applied to 3D objects to change their position, orientation, or size. However, the introduction of the z-axis requires more complex mathematical operations to simulate how objects behave in 3D space.

• Translation involves moving an object along the x, y, and z axes.
• Rotation can be applied around any of the three axes, allowing objects to spin or tilt in space.
• Scaling adjusts the size of an object, either uniformly or non-uniformly along each axis.

In 3D graphics, objects must also be projected onto a 2D surface (such as a computer screen) for viewing.

• Perspective projection simulates how objects appear smaller as they move farther away from the viewer, creating a sense of depth.
• Alternatively, orthographic projection maintains the size of objects regardless of their distance from the viewer, often used in technical illustrations.

Rendering

The process of creating a final image from geometric data is known as rendering. Rendering converts 3D models and scenes into 2D images that can be displayed on a screen or printed.

Rasterization

One of the most common rendering techniques is rasterization, where 3D objects are converted into pixels on a 2D screen. In this process −

• Vertices − The vertices of 3D models are projected onto the screen space.
• Triangles − The geometry of the models is broken down into triangles, as these are the simplest polygons to work with.
• Pixels − Each triangle is filled with the appropriate colors, lighting, and textures, resulting in the final pixelated image.

Rasterization has limitations, especially when dealing with complex lighting and reflections.

Ray Tracing

For more realistic rendering, techniques like ray tracing are used. Ray tracing simulates the behavior of light by tracing the path of individual rays as they interact with objects in a scene. This method can produce highly realistic images with accurate shadows, reflections, and refractions.

However, ray tracing is computationally expensive and it requires significant processing power, which is why it has historically been used in offline rendering. Recent advancements in real-time ray tracing have made it more accessible for interactive applications like gaming.

Conclusion

In this chapter, we covered the basic concepts of images, pixels, and geometry in computer graphics. Pixels represent the smallest unit of visual data, while geometry defines the shape and structure of objects within an image. Rendering techniques bridge these two components, transforming abstract geometric representations into detailed, visually compelling images.