Perspective Projection in Computer Graphics

---

---

The concept of perspective projection is quite different from parallel projection. Perspective projection is one of the most frequently used methods for rendering realistic images.

Unlike orthographic and oblique projections, perspective projection mimics how human vision works by representing objects smaller as they move farther away from the viewer. This creates a sense of depth and realism in the image.

In this chapter, we will see the concept of perspective projection, its importance in creating realistic 3D visualizations, and the different types of perspective projections. We will also cover the mathematical foundations for a better understanding.

What is Perspective Projection?

Like any projection methods, it is kind of projecting 3D objects onto a 2D plane. But in such a way that objects farther from the viewer appear smaller, and objects closer appear larger. This technique replicates the way the human eye perceives the world. It is like images appear more realistic by adding depth. Perspective projection lines converge at a single point, two point or three points based on their types. These points are known as the vanishing point.

Types of Perspective Projection

There are three main types of perspective projection based on the number of vanishing points used in the projection:

• One-Point Perspective Projection
• Two-Point Perspective Projection
• Three-Point Perspective Projection

Each type of projection offers a different way to represent 3D objects on a 2D plane. This is depending on the viewing angle and the complexity of the scene.

1. One-Point Perspective Projection

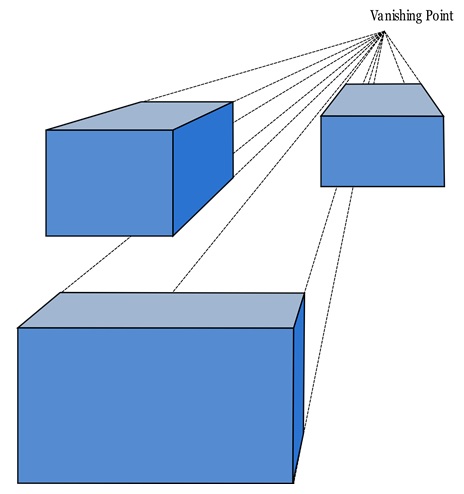
In one-point perspective projection, all lines perpendicular to the viewer converge toward a single vanishing point on the horizon. This type of projection is used when the object is directly facing the viewer, and the parallel lines move away from the observer. Illusion is they are converges at a single point.

One-point perspective is simple and commonly used in scenes where one face of the object is aligned directly with the viewer, such as looking down a straight road, hallway, or railroad tracks. The front face of the object is undistorted, while the other sides appear to recede toward the vanishing point.

Example

Take a look at the following projection −

Mathematical Representation

In one-point perspective, the projection formulas for the 2D coordinates (x, y)of a 3D point (x,y, z) are −

$$\mathrm{x' \:=\: \frac{x}{1 \:+\: \frac{z}{d}}}$$

$$\mathrm{y' \:=\: \frac{y}{1 \:+\: \frac{z}{d}}}$$

Where,

• d is the distance from the viewer to the projection plane.
• z represents the depth of the point from the viewer.

2. Two-Point Perspective Projection

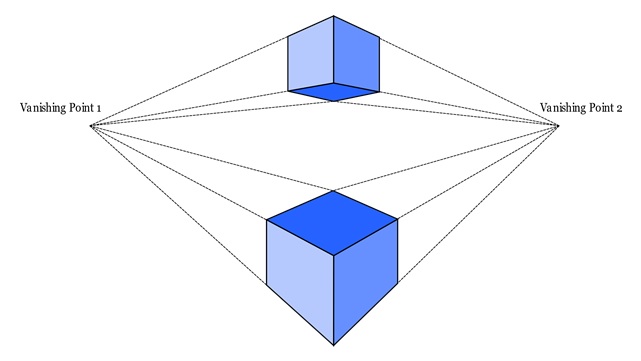
Two-point perspective projection is more common for objects that are not aligned directly with the viewer. In this method, there are two vanishing points on the horizon line, usually representing the convergence of lines in two directions (e.g., width and depth). This type of projection is used when the object is rotated so that none of its faces are directly facing the viewer.

In two-point perspective, vertical lines remain parallel, but horizontal lines recede toward two separate vanishing points. This type of projection is frequently used in architectural drawings, where buildings are viewed at an angle, showing two sides of the structure.

Example

Let us see the following figure of 2-point perspective −

Mathematical Representation

In two-point perspective, the projection formulas for a 3D point (x, y, z) are −

$$\mathrm{x' \:=\: \frac{x}{1 \:+\: \frac{z}{d_1}}}$$

$$\mathrm{y' \:=\: \frac{y}{1 \:+\: \frac{z}{d_2}}}$$

Where, d1 and d2 are the distances from the viewer to the two vanishing points.

3. Three-Point Perspective Projection

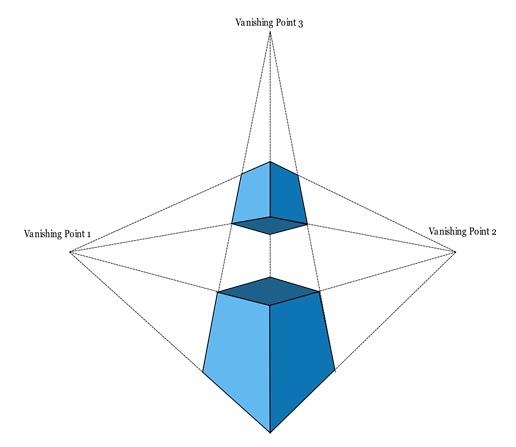
Three-point perspective projection is another type. This is used when none of the object's axes are parallel to the projection plane. In this method, there are three vanishing points: two on the horizon (representing width and depth) and one either above or below the object (representing height). This type of perspective is often used when the viewer is looking up at a tall structure or down from a high viewpoint.

In three-point perspective, all three axes (width, height, and depth) converge toward separate vanishing points. This creates a dramatic and dynamic view of objects, such as skyscrapers or tall buildings viewed from a low angle.

Example

Take a look at the following projection −

Mathematical Representation

In three-point perspective, the projection formulas for the 2D coordinates (x, y)of a 3D point (x, y, z) are −

$$\mathrm{x' \:=\: \frac{x}{1 \:+\: \frac{z}{d_1}}}$$

$$\mathrm{y' \:=\: \frac{y}{1 \:+\: \frac{z}{d_2}}}$$

$$\mathrm{z' \:=\: \frac{z}{1 \:+\: \frac{z}{d_3}}}$$

Where, d1, d2, and d3 represent the distances to the three vanishing points.

Perspective Projection Matrix

The general form of a perspective projection matrix is −

$$\mathrm{P_{\text{perspective}} \:=\: \begin{bmatrix} \frac{1}{z_f} & 0 & 0 & 0 \\ 0 & \frac{1}{z_f} & 0 & 0 \\ 0 & 0 & \frac{z_f}{z_f - z_n} & 0 \\ 0 & 0 & \frac{-z_n z_f}{z_f - z_n} & 1 \end{bmatrix}}$$

Where,

• z_f is the distance to the far clipping plane.
• z_n is the distance to the near clipping plane.

This matrix transforms the 3D coordinates of an object into 2D coordinates for display on a screen or other 2D medium.

Advantages of Perspective Projection

Following are the advantages of Perspective Projection −

• Realistic Representation − Perspective projection provides a realistic representation of 3D objects, as it mimics the way human vision works. The use of vanishing points creates the illusion of depth, making the objects appear more lifelike.
• Depth Perception − One of the key advantages of perspective projection is the addition of depth perception. Objects farther from the viewer appear smaller, and closer objects appear larger, giving a strong sense of distance in the scene.
• Widely Used in Visual Media − Perspective projection is widely used in 3D graphics, video games, virtual reality, and animations to create realistic environments. It is also essential in fields like architecture and engineering, where accurate 3D visualizations are important.

Limitations of Perspective Projection

Following are the limitations of Perspective Projection −

• Complexity − Compared to orthographic or oblique projection, perspective projection is mathematically more complex. It requires more calculations to determine the position of each point in the image, making it computationally intensive.
• Distortion at Extreme Angles − When objects are very close to the vanishing points, they may appear distorted or stretched. This can be problematic in some applications where precision is important.
• Not Suitable for Technical Drawings − While perspective projection is ideal for realistic visualizations, it is not suitable for technical or engineering drawings where accurate measurements and dimensions are required. For these purposes, orthographic projection is preferred.

Conclusion

Perspective projection is a useful technique used for representing 3D objects realistically on a 2D plane. We explained the three main types of perspective projection: one-point, two-point, and three-point perspective with examples and mathematical understanding, each with its own applications depending on the complexity of the scene. We also covered the projection matrix, and how objects are transformed into 2D coordinates. Finally, we highlighted the advantages and limitations of perspective projection.