Rotation with Quaternions in Computer Graphics

---

---

3D transformations are the techniques used to translate, rotate, scale, reflect objects in 3D space. For 3D rotation, it gets quite interesting and requires a pivotal axis. Here, Euler rotation faces some problems. For that reason, there is another concept of Quaternion. Quaternions provide an efficient way to handle these rotations.

In this chapter, we will see the problems of Euler rotation then how quaternions are used for rotation in 3D space. We will see mathematical details for a clear understanding.

Problem of Euler Angle Rotation in 3D

As we know for rotation, we need three axes and on them we can apply the rotations. For a certain rotation, it must follow an order and consecutive rotations around the x, y, and z axes. This method is easy but it has significant drawbacks. One of the biggest issues is gimbal lock. Gimbal lock occurs when two of the three rotation axes align after a certain rotation. Now it causes the system to lose a degree of freedom. It can no longer rotate freely in all directions.

Let us see the Euler rotation axes in normal case −

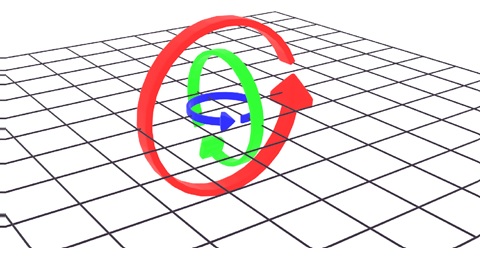
If we consider the rotation order x, y, z, then if we rotate x by 90, then rotate y as 90, x and y will be on same plane. And form a gimbal lock.

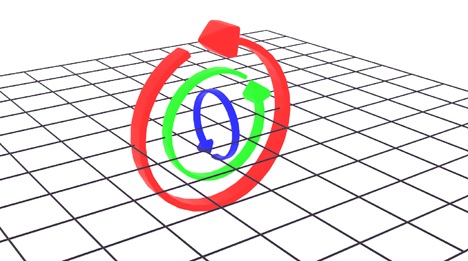
Then after rotating z to 90 again, all three will be in same plane, this is also the gimbal lock situation.

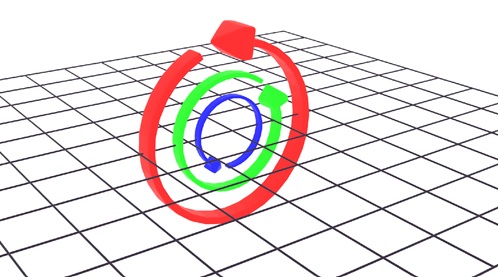
Now rotating any axis does affect rotation on the same plane. Which is not desirable.

Solve using Quaternions

Quaternions address this issues effectively. Unlike Euler angles, quaternions do not suffer from gimbal lock because they represent rotations in a four-dimensional space. This allows smooth and continuous movement without losing any degrees of freedom.

Position and Orientation

We understood the problem with figures, let us understand it in a more theoretical aspect. When we talk about an object in 3D space, we need to define both its position and orientation. The position is typically represented by Cartesian coordinates (x, y, z). Orientation, on the other hand, is the rotation from a standard unrotated position to its current rotated state.

There are several ways to represent this orientation −

• Euler angles
• Rotation vectors (axis/angle)
• 3x3 matrices
• Quaternions

Among these, quaternions are highly effective

Idea of Quaternions

Quaternions are an extension of complex numbers. In simple terms, quaternions consist of four components: one scalar (real number) and a 3D vector. This 4D entity allows for the efficient representation of 3D rotations.

A quaternion, q, can be written as −

$$\mathrm{q \:=\: w \:+\: x \hat{i} \:+\: y \hat{j} \:+\: z \hat{k}}$$

Where,

• w is the scalar part
• (x,y,z) forms the vector part

To use quaternions for representing orientations, we often deal with unit quaternions. A unit quaternion has a magnitude of 1 and lies on the surface of a 4D hypersphere.

Rotation with Quaternions

Representing Rotations − To represent a rotation by an angle around an axis a = (ax, ay, az) using quaternions, we use the following unit quaternion formula −

$$\mathrm{q \:=\: \cos\left(\frac{\theta}{2}\right) \:+\: \sin\left(\frac{\theta}{2}\right)\left(a_x \hat{i} \:+\: a_y \hat{j} \:+\: a_z \hat{k}\right)}$$

Here,

• θ is the rotation angle
• (a_x, a_y, a_z) is the unit vector representing the axis of rotation

This quaternion q encapsulates the rotation we want to apply to an object.

Quaternion Multiplication

One of the key operations with quaternions is multiplication. If we have two quaternions, q1 and q2, representing two rotations, their product q1 × q2 gives a new quaternion that combines both rotations.

Quaternion multiplication is similar to matrix multiplication in that it is not commutative. That means the order of multiplication matters: q1 × q2 does not equal q2 × q1 .

Rotating a Vector with Quaternions

To rotate a vector v using a quaternion q, we use quaternion conjugation. First, represent the vector as a quaternion −

$$\mathrm{\mathbf{v_q} \:=\: 0 \:+\: v_x \hat{i} \:+\: v_y \hat{j} \:+\: v_z \hat{k}}$$

Then, the rotated vector is given by −

$$\mathrm{vq' \:=\: q\: \times\: vq\: \times\: q^{-1}}$$

Where q⁻¹ is the inverse of the quaternion q. The result is a new quaternion v_q′ and the vector part of this quaternion represents the rotated vector.

Example of Rotating a Vector in 3D

Let us consider an example to understand how quaternions perform a 3D rotation. Suppose we want to rotate a vector v = (1, 0, 0) by 90 degrees around the z-axis a=(0, 0, 1).

Step 1: Represent the Rotation as a Quaternion

First, we need to represent the 90-degree rotation around the z-axis using a quaternion. The quaternion for this rotation is −

$$\mathrm{q \:=\: \cos \left( \frac{90}{2} \right) \:+\: \sin \left( \frac{90}{2} \right) \left( 0i \:+\: 0j \:+\: 1k \right)}$$

It simplifies to,

$$\mathrm{q \:=\: 0.707 \:+\: 0.707k}$$

Step 2: Represent the Vector as a Quaternion

Next, we represent the vector v=(1, 0, 0) as a quaternion −

$$\mathrm{vq \:=\: 0 \:+\: 1i \:+\: 0j \:+\: 0k \:=\: i}$$

Step 3: Apply the Rotation

Now, we perform the quaternion multiplication to rotate the vector −

$$\mathrm{vq' \:=\: q \:\times\: vq \:\times\: q^{-1}}$$

First, calculate the inverse of q −

$$\mathrm{q^{-1} \:=\: 0.707 \:-\: 0.707k}$$

Then, multiply,

$$\mathrm{vq' \:=\: (0.707 \:+\: 0.707k) \:\times\: i\: \times\: (0.707 \:-\: 0.707k)}$$

Simplifying the multiplication results in the new quaternion −

$$\mathrm{vq' \:=\: 0 \:+\: 0i \:+\: 1j \:+\: 0k}$$

This corresponds to the vector v′ = (0, 1, 0), which is the original vector rotated by 90 degrees around the z-axis.

Interpolation with Quaternions

Another interesting field where quaternion is used is the interpolation. Interpolating between two rotations, quaternions provide a smooth transition through spherical linear interpolation (slerp). Instead of simply blending between two angles, slerp traces a path along the surface of a 4D sphere. This is resulting in a smoother and more visually appealing rotation.

Spherical Linear Interpolation (SLERP)

Given two unit-quaternions q1 and q2, slerp provides a way to interpolate between them −

$$\mathrm{\text{slerp}(q_1, q_2, t) \:=\: \frac{\sin((1 \:-\: t) \Omega)}{\sin \Omega} q_1 \:+\: \frac{\sin(t \Omega)}{\sin \Omega} q_2}$$

Where Ω is the angle between the two quaternions and t is the interpolation parameter, ranging from 0 to 1.

This method states that the interpolation follows the shortest path, or the great arc, between the two quaternions on the 4D hypersphere.

Conclusion

In this chapter, we covered the concept of rotations in computer graphics using quaternions. We understood the Euler angle problems of gimbal lock and how quaternions solve them, followed by the basics of how quaternions represent rotations.

We also looked at a practical example of rotating a vector using quaternions and discussed the concept of quaternion interpolation for smooth transitions between rotations.