Deformation Animation in Computer Graphics

---

---

Keyframe and motion path animations are used for showing displacement and transition. Morphing, as discussed in the previous chapter, highlights changing in shape. There is another type of animation where we focus on changing in shape; it is known as deformation.

Deformation is usually associated with modeling but is often discussed as part of animation because of how it helps create dynamic effects. Read this chapter to learn the basic principles of deformations in animation. Here you will also find a set of examples, focusing on bend, twist, and taper.

Basics of Deformations

Deformation in animation is about changing the shape of an object over time. This can be done by applying functions to the vertices or control points that make up the object. These points are often part of a mesh or a spline surface, and the function repositions them to create a new shape.

In simple terms, a mathematical function, represented as p = f(p, γ), is applied to each point. Here, p is the original point, and γ is a vector of parameters used by the deformation function. Various functions can be chosen to achieve different effects, such as bending, twisting, and tapering the object. One of the key advantages of this approach is the ease of animating deformations by keyframing the parameters of the function.

However, there are challenges to this technique. One challenge is selecting the right mathematical function for unusual deformations. Another issue is that this method tends to cause global deformation. The entire object is reshaped rather than just a specific part. This limitation can make it difficult to create precise, localized changes.

Global Deformations: Bend, Twist, and Taper

The three popular examples of global deformations are bend, twist, and taper. These functions change the shape of the entire object, and their parameters can be animated to create dynamic shape changes.

• Bend changes the curvature of the object.
• Twist rotates one end of the object while keeping the other end stationary.
• Taper gradually reduces or increases the width or thickness of the object.

Let us see the following figure which illustrates these deformations, showing how they work on an object.

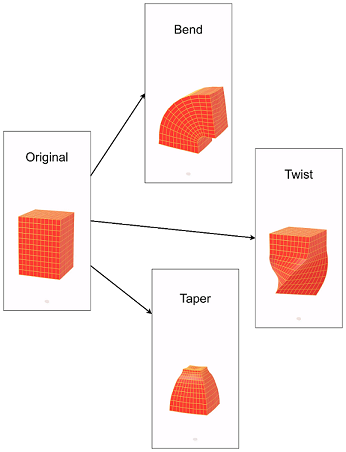
While these are simple deformations, they can be combined to create complex effects in animation.

Let us see these deformations one by one in true animations.

1. The Bend

2. The Twist

3. The Taper

Local Deformations

In contrast to global deformations, there are local deformations too. They offer more control over the specific parts of an object. A common approach is to move a single vertex and then adjust neighbouring vertices to follow the lead vertex. This technique uses an attenuation function that controls the amount of deformation, with the influence of decreasing as the distance from the seed vertex increases. Attenuation is often computed over the surface of the object.

Local deformations are especially useful for producing more natural and realistic shape changes. For example, animators can use local deformations to create effects such as squashing, stretching, or bulging specific areas of an object without affecting the entire form. These effects are common in character animation, where subtle changes in facial expressions or body movements are needed.

Free-Form Deformation

Another important part is the free-form deformation (FFD). It was introduced by Sederberg and Parry in 1986. FFD are allowed for smooth, detailed deformations using a grid-based system. It is especially useful for creating complex shape changes while maintaining smoothness across the object.

In FFD, a rectilinear grid is placed around the object or part of the object that needs to be deformed. Each point within this grid is assigned a set of coordinates, typically labelled s, t, and u. The animator can then freely manipulate the grid, distorting it into new shapes. As the grid changes, the shape of the object also changes. The points on the object are recalculated based on their new positions within the distorted grid.

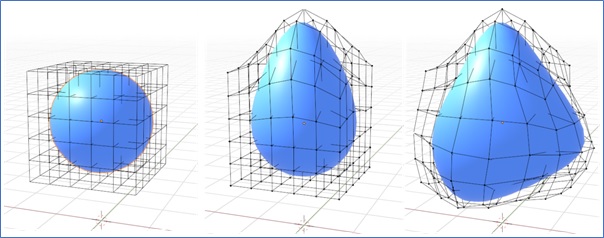
The deformed object is reconstructed using the coordinates from the original undistorted grid and the newly shaped lattice points. This process is similar to Bzier interpolation, where control points determine the shape of the curve or surface. The distorted lattice points act as control points, allowing for smooth deformations.

Advantages of Free-Form Deformation

A significant advantage of FFD is that it allows animators to work with a low-resolution version of the object while making deformations. This is helpful when animating complex objects since it simplifies the control over the object's shape. Once the lattice grid is adjusted, the deformation is applied to the high-resolution object, resulting in a smooth and visually appealing shape change.

Additionally, FFD grids can be treated as objects themselves and can be transformed, animated, or even further deformed. This flexibility given by FFD makes it as versatile tool for animation.

Combining Deformations

The deformation could be combined together. To create more intricate effects. For example, animators can apply a bend deformation followed by a twist. Or they can use local deformations within an FFD grid for more detailed adjustments.

The ability to blend multiple deformations allows for greater creativity and realism in animated sequences. By using both global and local deformations, animators can fine-tune the shape changes to match the desired outcome.

Challenges in Deformation Animation

We have seen several advantages of deformation. There are several challenges as well. One major issue is finding the right mathematical function to achieve the desired effect, especially for nonstandard deformations. Some complex deformations may require custom functions or combinations of existing methods.

Another challenge is maintaining control over how much of the object is affected. Global deformations affect the entire object, which can be limiting when trying to isolate certain areas for change. Local deformations provide more control, but they also require more precision and careful attention to detail.

FFD helps overcome some of these challenges by offering flexibility and control, but it requires a good understanding of how to manipulate the lattice grid effectively. Animators need to balance the ease of use with the complexity of achieving realistic, natural-looking deformations.

Conclusion

In this chapter, we explained the basics of deformations and how functions like bend, twist, and taper are used to create shape changes. Then, we understood local deformations, which offer more control and precision, and how keyframing plays a role in animating these changes.

In addition, we covered the free-form deformation technique that provides a flexible and powerful way to manipulate shapes using a grid-based system. Finally, we looked at some of the challenges associated with deformation animation and the importance of combining different techniques for greater creativity.