Scene Graphs in Computer Graphics

---

---

Scene graphs are used to manage and organize complex scenes. They help arrange objects, especially when transformations like rotation, translation, or scaling are involved. By using a hierarchical structure, scene graphs make it easier to manipulate objects in a scene. Read this chapter to understand the basics of scene graphs.

What is a Scene Graph?

A scene graph is a way to organize objects within a scene, often in a hierarchical structure. When working with objects in computer graphics, transformations (such as rotating, moving, or scaling) need to be applied to place objects correctly in the scene. In simpler scenes it can be managed manually, but for complex scenes it needs a structured way to handle many transformations.

Scene graphs consist of nodes. Each node represents either an object or a transformation. Nodes are arranged in a parent-child relationship. This means that a transformation applied to a parent node affects all its child nodes. This hierarchical structure allows transformations to be efficiently managed and makes it easier to modify the scene.

Understanding Scene Graphs with the Hinged Pendulum

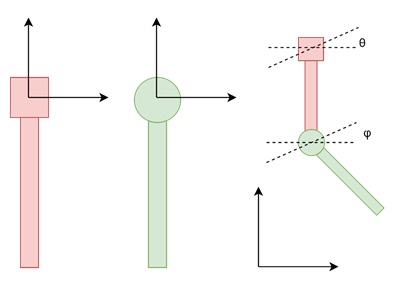
To better understand how scene graphs work, let us consider an example of a hinged pendulum. The pendulum consists of two parts: an upper part and a lower part, connected by a hinge.

Local and Global Transformations

Each part of the pendulum has its own local coordinate system. For example, if we want to move or rotate the upper part of the pendulum, we apply transformations like rotation and translation in its local coordinates.

Upper Pendulum

Rotate the upper pendulum by an angle θ (theta). Translate it to a position p. This transformation can be represented by a composite matrix, M₃, which is the product of the rotation and translation matrices −

$$\mathrm{M_1 \:=\: \text{rotate }(\theta)}$$

$$\mathrm{M_2 \:=\: \text{translate }(p)}$$

$$\mathrm{M_3 \:=\: M_2\: \times\: M_1}$$

We apply this matrix to the upper pendulum, placing it correctly in the scene.

Managing the Lower Pendulum

The lower pendulum is more complicated. It is attached to the upper pendulum at a specific point, in the upper pendulums local coordinate system. The transformation for the lower pendulum involves −

• Rotating it by an angle φ (phi).
• Moving it so that its hinge aligns with the given point.

The composite transformation matrix for the lower pendulum is −

$$\mathrm{M_a \:=\: \text{rotate }(\varphi)}$$

$$\mathrm{M_b \:=\: \text{translate }(b)}$$

$$\mathrm{M_c \:=\: M_b\: \times \:M_a}$$

$$\mathrm{M_d \:=\: M_3\: \times \:M_c}$$

We apply Md to all the points of the lower pendulum. The lower pendulum moves along with the upper pendulum because its transformations are dependent on those of the upper part. This demonstrates the hierarchical nature of the scene graph.

Building the Scene Graph

In the case of the hinged pendulum, the scene graph helps to manage the relationship between the upper and lower pendulums. In the following figure shows the scene graph for this system.

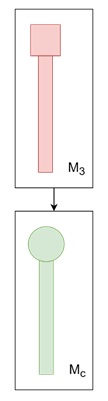
In this graph, each transformation is represented as a node, and the hierarchy reflects how each objects transformation depends on its parent. The transformation for the lower pendulum depends on the upper pendulums transformation. Therefore, when the upper pendulum moves or rotates, the lower pendulum follows. This is automatically handled by the scene graph structure.

Scene Graphs in More Complex Scenes

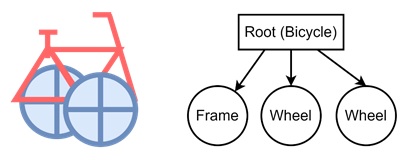
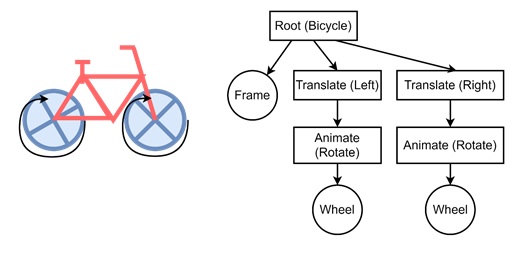
Consider a cycle has three components, the frame, and two wheels. The initial scene graph contains the root, then it is holding three children, frame, wheel, and wheel. From this basic graph we will increase this later on.

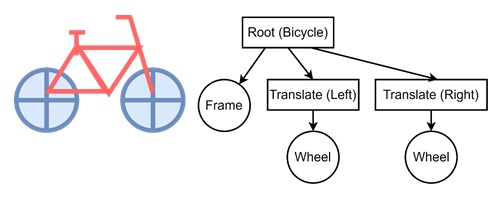
Now translate the first wheel to the left and second wheel to the right to form the proper bicycle. For that we need to translate block. After completing the bicycle, it will be ready for rotating wheels.

For rotation, we are adding the rotation nodes inside the scene graph. After translate it is animating for both the wheels. It is ready for moving bicycle now.

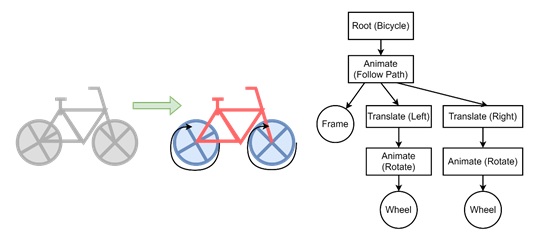
See in the following frame, it is following a path. For that we need the whole bicycle setup. After root, it is animating block then after that rest of the nodes are working like the same.

Recursive Traversal of a Scene Graph

Scene graphs are often traversed recursively. The function that performs this traversal operates on each node of the graph, applying the transformation matrices in the correct order. The basic steps of the traversal are as follows −

• Push the local transformation matrix onto the matrix stack.
• Draw the object using the composite matrix from the stack.
• Recursively traverse the child nodes of the current node.
• Pop the matrix after finishing with the current node.

Conclusion

In this chapter, we explained the basic concept of scene graphs in computer graphics. We started with the basics of scene graphs and how they manage transformations. Using the example of a hinged pendulum, we saw how transformations can be applied hierarchically.

We also looked at a more complex scene of bicycle system to show how scene graphs can manage many objects and transformations. Finally, we discussed matrix stacks and how they are used to efficiently implement scene graphs.