
- Computer Graphics - Home
- Computer Graphics Basics
- Computer Graphics Applications
- Graphics APIs and Pipelines
- Computer Graphics Maths
- Sets and Mapping
- Solving Quadratic Equations
- Computer Graphics Trigonometry
- Computer Graphics Vectors
- Linear Interpolation
- Computer Graphics Devices
- Cathode Ray Tube
- Raster Scan Display
- Random Scan Device
- Phosphorescence Color CRT
- Flat Panel Displays
- 3D Viewing Devices
- Images Pixels and Geometry
- Color Models
- Line Generation
- Line Generation Algorithm
- DDA Algorithm
- Bresenham's Line Generation Algorithm
- Mid-point Line Generation Algorithm
- Circle Generation
- Circle Generation Algorithm
- Bresenham's Circle Generation Algorithm
- Mid-point Circle Generation Algorithm
- Ellipse Generation Algorithm
- Polygon Filling
- Polygon Filling Algorithm
- Scan Line Algorithm
- Flood Filling Algorithm
- Boundary Fill Algorithm
- 4 and 8 Connected Polygon
- Inside Outside Test
- 2D Transformation
- 2D Transformation
- Transformation Between Coordinate System
- Affine Transformation
- Raster Methods Transformation
- 2D Viewing
- Viewing Pipeline and Reference Frame
- Window Viewport Coordinate Transformation
- Viewing & Clipping
- Point Clipping Algorithm
- Cohen-Sutherland Line Clipping
- Cyrus-Beck Line Clipping Algorithm
- Polygon Clipping Sutherland–Hodgman Algorithm
- Text Clipping
- Clipping Techniques
- Bitmap Graphics
- 3D Viewing Transformation
- 3D Computer Graphics
- Parallel Projection
- Orthographic Projection
- Oblique Projection
- Perspective Projection
- 3D Transformation
- Rotation with Quaternions
- Modelling and Coordinate Systems
- Back-face Culling
- Lighting in 3D Graphics
- Shadowing in 3D Graphics
- 3D Object Representation
- Represnting Polygons
- Computer Graphics Surfaces
- Visible Surface Detection
- 3D Objects Representation
- Computer Graphics Curves
- Computer Graphics Curves
- Types of Curves
- Bezier Curves and Surfaces
- B-Spline Curves and Surfaces
- Data Structures For Graphics
- Triangle Meshes
- Scene Graphs
- Spatial Data Structure
- Binary Space Partitioning
- Tiling Multidimensional Arrays
- Color Theory
- Colorimetry
- Chromatic Adaptation
- Color Appearance
- Antialiasing
- Ray Tracing
- Ray Tracing Algorithm
- Perspective Ray Tracing
- Computing Viewing Rays
- Ray-Object Intersection
- Shading in Ray Tracing
- Transparency and Refraction
- Constructive Solid Geometry
- Texture Mapping
- Texture Values
- Texture Coordinate Function
- Antialiasing Texture Lookups
- Procedural 3D Textures
- Reflection Models
- Real-World Materials
- Implementing Reflection Models
- Specular Reflection Models
- Smooth-Layered Model
- Rough-Layered Model
- Surface Shading
- Diffuse Shading
- Phong Shading
- Artistic Shading
- Computer Animation
- Computer Animation
- Keyframe Animation
- Morphing Animation
- Motion Path Animation
- Deformation Animation
- Character Animation
- Physics-Based Animation
- Procedural Animation Techniques
- Computer Graphics Fractals
4 and 8 Connected Polygon in Computer Graphics
In the last two chapters, we covered the Flood Fill and Boundary Fill algorithms that are used for filling a polygon. There are multiple such methods for filling polygons. In this chapter, we will focus on the 4-connected method and 8-connected methods. We will see how the 4connected and 8-connected polygons look like, using animated gifs and also discuss their limitations.
4-Connected and 8-Connected Polygon
While filling a polygon we choose neighbouring pixels. Pixels are arranged in a grid. Each pixel has neighbouring pixels, and the way these neighbours are considered connected is essential for tasks like filling, smoothing, or detecting shapes.
The concept of 4-connected and 8-connected polygons works based on the way pixels inside a polygon are related to one another based on their neighbours.
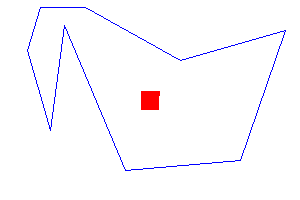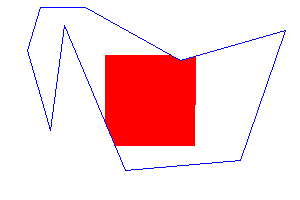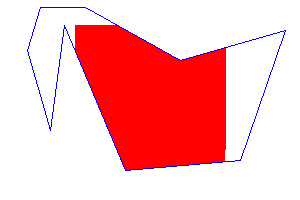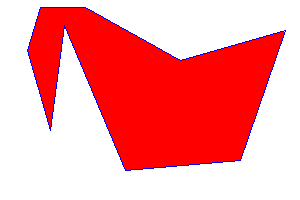
4-Connected Polygon
In a 4-connected polygon, each pixel is connected to four of its neighbouring pixels: left, right, above, and below. The diagonals are not considered connected in this case. When filling or processing a polygon, the algorithm only checks these four neighbouring pixels.
Neighbours in a 4-connected grid −
- (x-1, y) → Left
- (x+1, y) → Right
- (x, y-1) → Above
- (x, y+1) → Below
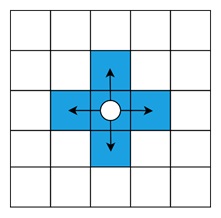
This type of connection is simpler and faster to compute because fewer neighbours are involved. However, it may result in gaps or missed pixels along the diagonal edges when filling polygons with more complex or slanted boundaries.
Example of 4-Connected Polygon
In a 4-connected polygon, the pixel P is only connected to the four adjacent pixels directly on its left, right, top, and bottom. The diagonal pixels are not connected. See the following animated gif where this is being displayed for actual graphics components.
8-Connected Polygon
Another variation is the 8-connected polygon. This expands on this by connecting each pixel to its eight surrounding neighbours. This includes the four diagonal neighbours in addition to the four directly adjacent ones. This method ensures that the entire area is connected, especially in cases where diagonal connections are important.
Neighbours in an 8-connected grid −
- (x-1, y) → Left
- (x+1, y) → Right
- (x, y-1) → Above
- (x, y+1) → Below
- (x-1, y-1) → Top-left diagonal
- (x+1, y-1) → Top-right diagonal
- (x-1, y+1) → Bottom-left diagonal
- (x+1, y+1) → Bottom-right diagonal
Because all surrounding pixels are considered connected, this approach provides more continuous coverage when filling shapes, particularly along the edges.
Example of 8-Connected Grid
In an 8-connected polygon, pixel P is connected to all eight surrounding pixels: four direct neighbours and four diagonal neighbours. See the following animated gif where this is being displayed for actual graphics components.
Differences between 4-Connected and 8-Connected Polygon
The following table highlights the major differences between 4-connected and 8-connected polygons −
| 4-Connected Polygons | 8-Connected Polygons |
|---|---|
| Considers only four neighbors: left, right, top, and bottom. | Considers eight neighbors: four direct and four diagonal. |
| Simpler and faster to compute. | More complex but provides better coverage. |
| May leave gaps along diagonal edges. | Fills areas more completely, including diagonals. |
| Useful for basic shapes and simple filling. | Ideal for more complex shapes and continuous filling. |
Overflowing Case for 8-Connected Filling
Though these two methods (4-connected and 8-connected Filling) work fine for polygon filling, but there are some cases where we may face some unwanted cases. When a polygon starts filling, it checks the edge pixels of the polygon color and accordingly it expands or stops. Now let us see the following figure where it fails.
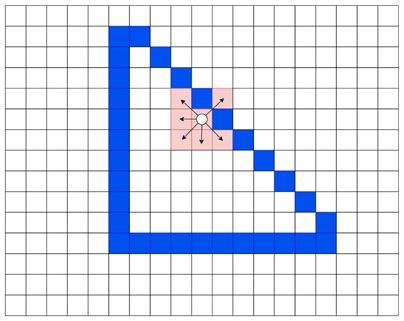
Here, the blue boundary is forming the polygon. Now, we are filling with pink color. The point with dot is expanding. Its top and right points are blue, so it will stop expanding on these directions, but it will see the top-left corner is free cell, and it has no idea that it is outside the region, so it will color them.
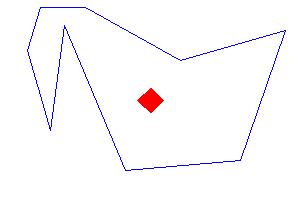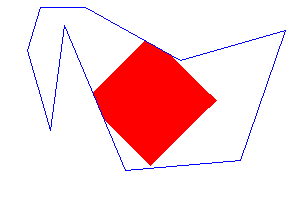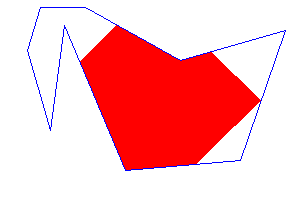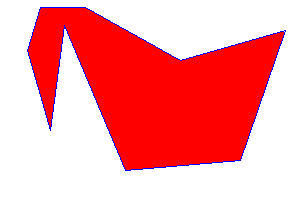
After coloring the pixel outside the region, it will lead to overflow. It will fill the other blank region with colors which is not intended. Let us see this effect in real graphics scenario.
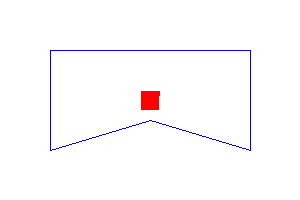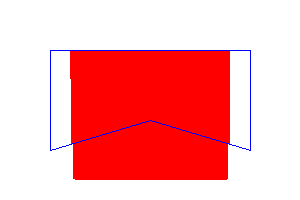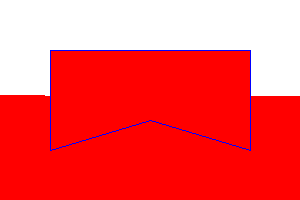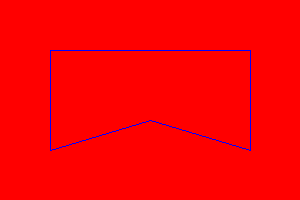
To solve this issue, we need safe diagonal check. We need to give a special care when assigning the diagonals by checking the diagonal is outside or inside the region.
Conclusion
In this chapter, we explained the concept of 4-connected and 8-connected polygons in computer graphics. These methods define how pixels are connected inside a polygon. It is essential to learn this concept to understand various graphics tasks such as filling, boundary detection, and image segmentation.
While 4-connected polygons are faster and simpler, they may leave gaps along diagonal edges. On the other hand, 8-connected polygons provide more comprehensive coverage. We also covered the concept of overflowing while filling diagonals, which can be solved using safe diagonal checking.