Binary Space Partitioning Trees in Computer Graphics

---

---

Binary Space Partitioning (BSP) trees are used for efficiently solving the visibility problem, mostly when dealing with planar polygons. Visibility is the challenge of determining which parts of a scene are visible from a particular viewpoint.

In computer games or other real-time rendering applications, managing visibility quickly and effectively is quite important for performance. BSP trees help by sorting and organizing objects in a scene to ensure that they are rendered in the correct order, from back to front. Read this chapter to learn the basics of BSP trees, how they work, and its basic algorithm.

What are BSP Trees?

The visibility problem arises when we have to decide the order in which objects in a scene should be drawn. The viewer only sees the parts of objects that are not hidden by others. The goal is to draw the objects in the correct order from back to front so that objects in front of others appear on top.

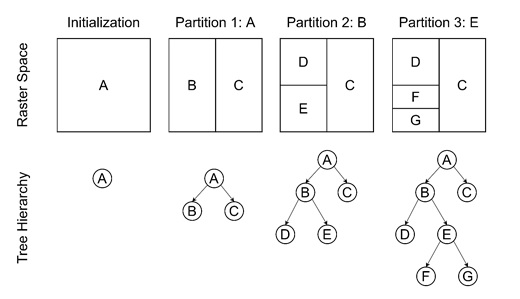
A BSP tree is a data structure that can be used to solve this problem efficiently. It is a type of spatial partitioning scheme where the space is divided into two halves using a plane. Each node in the BSP tree represents a partitioning plane, and the two child nodes represent the space on either side of the plane. The key idea behind BSP trees for visibility is that the scene is pre-processed into this tree structure, which can then be used to determine the visibility order of objects for any viewpoint.

The Binary Space Partitioning Tree Algorithm

The BSP tree algorithm is an example of the painter's algorithm. In the painters algorithm, objects are drawn in back-to-front order, so that objects closer to the viewer appear on top of those farther away. The BSP tree helps determine the correct order in which to draw the objects.

How the BSP Algorithm Works?

In the simplest form of the painter's algorithm −

• Sort objects back to front relative to the viewpoint.
• Draw each object on the screen in that order.

However, this approach can be complicated if the relative order of objects is not well defined. For example, consider three triangles arranged in a cycle, where each triangle partially overlaps another. In this case, there is no simple way to define a global back-to-front order.

The BSP tree algorithm solves this by recursively dividing the scene into two halves using a plane. This ensures that each object is on one side of a partitioning plane, and the correct drawing order can be determined by comparing the viewpoint with the position of the objects relative to the planes.

Building a Binary Space Partitioning Tree

Building a BSP tree indicates dividing the scene into a hierarchy of partitioning planes. Each plane divides the space into two halves: the positive side and the negative side. The objects are then sorted into the appropriate side, and the process is repeated recursively.

The Recursive Process

The process starts by selecting a polygon, say T1, and using it as the partitioning plane. All other polygons are sorted into two groups: those that lie on the positive side of the plane (where f1(p) > 0 and those that lie on the negative side (where f1(p) < 0). The tree is then built recursively by treating each group as a new set of polygons and repeating the process.

Handling Complex Cases

A problem arises when a polygon spans both sides of a partitioning plane. In this case, the polygon is split into two parts, each of which is placed in the appropriate side of the tree.

For example, if a triangle has two vertices on one side of the plane and one vertex on the other, it is divided into two smaller triangles.

This process of splitting means that every polygon can be placed in either the positive or negative side of the tree. The result is a tree where each node represents a polygon, and the tree can be traversed to determine the correct visibility order for any viewpoint.

Traversing a BSP Tree for Visibility

Once a BSP tree has been built, it can be used to determine the correct drawing order for any viewpoint. The process of traversing the tree is simple and efficient.

The Traversal Algorithm

The BSP tree traversal works by comparing the position of the viewpoint with the partitioning planes in the tree −

• Start at the root of the tree (which represents a partitioning plane).
• If the viewpoint is on the positive side of the plane, first draw the objects in the negative subtree, then draw the polygon at the current node, and finally draw the objects in the positive subtree.
• If the viewpoint is on the negative side of the plane, reverse the order: draw the objects in the positive subtree first, then the polygon at the current node, and finally the objects in the negative subtree.

This process states that objects are drawn in the correct order, from back to front, regardless of the viewpoint.

Optimizing BSP Trees

The efficiency of a BSP tree depends on how well it is constructed. Ideally, the tree should be balanced so that the number of nodes is minimized. However, in practice, the order in which polygons are added to the tree can affect its size and structure.

Triangle Splitting

One challenge for building a BSP tree is the need to split polygons that span both sides of a partitioning plane. Each time a polygon is split, it increases the number of nodes in the tree. To minimize this, it is needed to choose partitioning planes that reduce the need for splitting.

In some cases, it may be more efficient to use a polygon that divides the space without splitting too many other polygons. Finding the optimal partitioning plane is a complex problem and often requires a trade-off between tree size and computational efficiency.

Conclusion

BSP trees are used to solve the visibility problem in computer graphics. In this chapter, we covered the basic concept of BSP trees, how they divide space using partitioning planes, and how they help in determining the correct order to draw objects in a scene.

We also discussed the process of building and traversing a BSP tree and explained how to handle cases where polygons span multiple planes.