
- Computer Graphics - Home
- Computer Graphics Basics
- Computer Graphics Applications
- Graphics APIs and Pipelines
- Computer Graphics Maths
- Sets and Mapping
- Solving Quadratic Equations
- Computer Graphics Trigonometry
- Computer Graphics Vectors
- Linear Interpolation
- Computer Graphics Devices
- Cathode Ray Tube
- Raster Scan Display
- Random Scan Device
- Phosphorescence Color CRT
- Flat Panel Displays
- 3D Viewing Devices
- Images Pixels and Geometry
- Color Models
- Line Generation
- Line Generation Algorithm
- DDA Algorithm
- Bresenham's Line Generation Algorithm
- Mid-point Line Generation Algorithm
- Circle Generation
- Circle Generation Algorithm
- Bresenham's Circle Generation Algorithm
- Mid-point Circle Generation Algorithm
- Ellipse Generation Algorithm
- Polygon Filling
- Polygon Filling Algorithm
- Scan Line Algorithm
- Flood Filling Algorithm
- Boundary Fill Algorithm
- 4 and 8 Connected Polygon
- Inside Outside Test
- 2D Transformation
- 2D Transformation
- Transformation Between Coordinate System
- Affine Transformation
- Raster Methods Transformation
- 2D Viewing
- Viewing Pipeline and Reference Frame
- Window Viewport Coordinate Transformation
- Viewing & Clipping
- Point Clipping Algorithm
- Cohen-Sutherland Line Clipping
- Cyrus-Beck Line Clipping Algorithm
- Polygon Clipping Sutherland–Hodgman Algorithm
- Text Clipping
- Clipping Techniques
- Bitmap Graphics
- 3D Viewing Transformation
- 3D Computer Graphics
- Parallel Projection
- Orthographic Projection
- Oblique Projection
- Perspective Projection
- 3D Transformation
- Rotation with Quaternions
- Modelling and Coordinate Systems
- Back-face Culling
- Lighting in 3D Graphics
- Shadowing in 3D Graphics
- 3D Object Representation
- Represnting Polygons
- Computer Graphics Surfaces
- Visible Surface Detection
- 3D Objects Representation
- Computer Graphics Curves
- Computer Graphics Curves
- Types of Curves
- Bezier Curves and Surfaces
- B-Spline Curves and Surfaces
- Data Structures For Graphics
- Triangle Meshes
- Scene Graphs
- Spatial Data Structure
- Binary Space Partitioning
- Tiling Multidimensional Arrays
- Color Theory
- Colorimetry
- Chromatic Adaptation
- Color Appearance
- Antialiasing
- Ray Tracing
- Ray Tracing Algorithm
- Perspective Ray Tracing
- Computing Viewing Rays
- Ray-Object Intersection
- Shading in Ray Tracing
- Transparency and Refraction
- Constructive Solid Geometry
- Texture Mapping
- Texture Values
- Texture Coordinate Function
- Antialiasing Texture Lookups
- Procedural 3D Textures
- Reflection Models
- Real-World Materials
- Implementing Reflection Models
- Specular Reflection Models
- Smooth-Layered Model
- Rough-Layered Model
- Surface Shading
- Diffuse Shading
- Phong Shading
- Artistic Shading
- Computer Animation
- Computer Animation
- Keyframe Animation
- Morphing Animation
- Motion Path Animation
- Deformation Animation
- Character Animation
- Physics-Based Animation
- Procedural Animation Techniques
- Computer Graphics Fractals
3D Objects and Representation in Computer Graphics
There are many ways to represent 3D objects, depending on the type of object and the requirement of the system. Objects can range from geometrical shapes to complex forms like terrains, trees, or even the human body.
Read this chapter to get a clear understanding of the different methods of representing 3D objects in computer graphics.
Types of 3D Object Representations
3D objects in computer graphics can include shapes like polygons, splines, solid models, and more. The choice of representation depends on the complexity of the object and how it is used.
Some of the common types of 3D object representations are:
- Polygon Surfaces
- Spline Surfaces
- Procedural Methods
- Solid Object Models
- Physical Models
Each representation has unique features. These make it suitable for certain types of objects or environments. For example, terrain modelling procedural methods are good choice, while detailed modelling of a human body might involve spline surfaces or polygon meshes.
Polygon Surfaces
One of the most common methods used to represent 3D objects is polygon surfaces. These are used to represent the external surface of an object with a set of adjacent polygons. These surfaces are widely used because all the operations, such as intersection and normal calculations, are linear, which makes them fast and efficient for rendering.
Following are the advantages of using this method:
- Easy to handle mathematically
- Operations are linear, which is fast
- Non-polyhedron shapes can be approximated using polygon meshes
To represent a curved surface, a high number of small polygons can be used to make it appear smooth as shown in the following image.

Data Structures for Polygon Surfaces
To hold the data efficiently, suitable data structures are needed. These structures help manage important operations like intersection and normal calculations. The data structures also ensure the integrity of the polygon surfaces and allow for adding, changing, or removing vertices or polygons flexibly.
A common structure used is the Polygon Table which contains information about:
- Vertices
- Edges
- Polygons
These are stored in tables where each entry keeps track of adjacent polygons and vertices. Such structures are important for tasks like real-time rendering, where efficiency matters a lot.
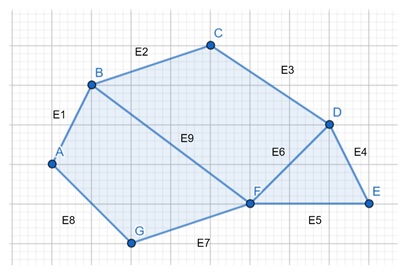
| Vertices | Edges | Surfaces |
|---|---|---|
| A: (2, 3, 0) | E1: AB | S1: E1, E9, E7, E8 |
| B: (3, 5, 0) | E2: BC | S2: E2, E3, E6, E9 |
| C: (6, 6, 0) | E3: CD | S3: E6, E4, E5 |
| D: (9, 4, 0) | E4: DE | |
| E: (10, 2, 0) | E5: EF | |
| F: (7, 2, 0) | E6: DF | |
| G: (4, 1, 0) | E7: FG | |
| E8: GA | ||
| E9: BF |
Spline Surfaces
The next useful representation is using curves. Here, spline surfaces used for representing 3D objects. A spline is a smooth curve defined by control points.
There are two main types of spline surfaces:
- Interpolated Splines − These pass through the control points.
- Approximated Splines − These do not necessarily pass through the control points but are guided by them.
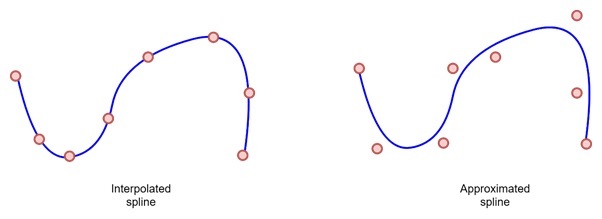
Splines are often used for representing smooth surfaces such as car bodies, terrain, and other organic shapes where sharp edges are not needed.
Solid Object Models
In some cases, representing just the surface of an object is not enough. For solid objects, we need models that describe the entire volume of the object, not just the surface. These are called solid object models, and they are used for applications like engineering simulations and 3D printing.
One such type is Constructive Solid Geometry (CSG). It is one of the key methods used to model solid objects. In this method, complex objects are constructed by combining simple shapes using set operations like intersection, union, and difference.
For example, we can combine a box and a cylinder using union or subtract the cylinder from the box to create complex shapes. CSG is especially useful in creating mechanical parts or architectural designs.
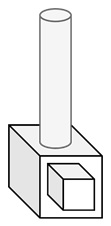
Sweep Representations
Another technique is sweeping representations, which involves creating a 3D object by sweeping a 2D shape along a path. This technique is often used to model objects like pipes, cables, or roads, where the cross-section remains the same along the length of the object. The following figure shows the idea.

Hierarchical Models
Another approach is Hierarchical models. These are used to represent complex objects made up of smaller, simpler shapes. These models organize the components into a structure like a tree. Each node of the tree represents an object, and complex objects are built by combining these simpler nodes. For example, a human figure can be modelled using hierarchical structures.
Each limb can be a node in the hierarchy, and the whole figure can be built by connecting these nodes.
Advanced 3D Representation Techniques
Aside from the standard techniques, some advanced methods are used for specific applications or to increase efficiency in rendering complex scenes. These include Scene Graphs, Octrees, and Fractal Geometry Methods.
Scene Graphs
A scene graph is a Directed Acyclic Graph (DAG) that is used to represent a scene or a complex object in a hierarchical manner. This is useful in real-time graphics where operations like picking objects, changing states, or handling animations require efficient management.
Octrees
Octrees are a data structure used for efficient representation of solid object volumes. The space is divided into eight equal parts (hence the name "octree"), and each division can be further divided recursively. Octrees are especially useful for handling large data sets, like medical images or geographical data.
Fractal Geometry Methods
In cases where natural, irregular objects need to be represented, fractal geometry methods can be used. These objects, like trees, mountains, or clouds, have a self-similar structure, meaning they look the same at different levels of detail.
For example, a tree can be modelled using fractals because the branches of a tree are similar in shape, whether viewed from close or far.
Conclusion
In this chapter, we explained the various methods used to represent 3D objects in computer graphics. We started with the basic types of objects and moved on to discuss common methods such as polygon surfaces, spline surfaces, and solid object models.
We also covered more advanced techniques like sweep representations, hierarchical models, scene graphs, octrees, and fractal geometry. Each method has its advantages depending on the type of object and the application.