Inside Outside Test in Computer Graphics

---

---

The Inside Outside Test is needed to check which part of the complex polygon is inside the region and which one is outside the region. We will see this in detail with examples for a better understanding.

Concept of Inside Outside Test

Area-filling algorithms and other graphics processes often need to identify interior regions of objects. Sometimes, it is not obvious which regions of the x-y plane are "interior" and which regions are "exterior" to the object.

This happens because in algorithms, the vertices of the area to be filled can be given in any order. This order does not tell us which region is interior and which is exterior. To solve this problem, we use inside outside tests.

Types of Inside Outside Test

There are two tests used to figure out if a region is interior or exterior −

• Odd-Even Rule, also known as the odd parity rule
• Non-zero Winding Number

Odd-Even Rule

Let us see the Odd-Even rule first. This rule helps us determine if a point is inside or outside a polygon. Imagine drawing a line from the point in question to a distant point outside the object. We then count how many times this line crosses the edges of the polygon.

• Odd Number of Crossings: The point lies inside the polygon.
• Even Number of Crossings: The point lies outside the polygon.

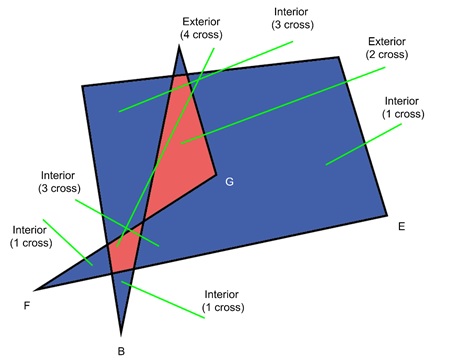
For the above given figure, there are 7 points A, B, C, D, E, F and G.

Condition for Odd-Even Rule

There is one important condition we must follow when using the Odd-Even rule. The line drawn from the point to the outside must not intersect a vertex or an endpoint of the polygon.

Example of Odd-Even Rule

Let us understand this rule with an example. Look at the image below. We have a polygon with a triangle inside. We want to figure out if different points lie inside or outside this polygon.

Imagine drawing lines from different points (A, B, C, D, E, F, G) to the outside. Count the number of edges each line crosses. Based on the Odd-Even rule, you can easily determine whether each point is interior (inside) or exterior (outside) the polygon.

Non-Zero Winding Number

The second method to test if a point is inside or outside a polygon is the Non-zero Winding Number method. This method requires understanding the direction of each edge in the polygon. Is it going clockwise or counter-clockwise?

The winding number is essentially the number of times the polygon's edges wind around a specific point in the counter-clockwise direction.

How to Apply Non-Zero Winding Number?

Here's how to apply the Non-zero winding number rule:

• Initial Value − Start with a winding number of 0.
• Draw a Line − Imagine drawing a line from the point in question to the outside, making sure it does not pass through any vertex (just like in the Odd-Even rule).
• Count Crossings −
  • Add 1 to the winding number for every edge that crosses the line from right to left (when viewed from the point towards the outside). This crossing represents a counter-clockwise movement.
• Subtract 1 from the winding number for every edge that crosses the line from left to right (when viewed from the point towards the outside). This crossing represents a clockwise movement.

Understanding Left to Right and Right to Left

The left to right and right to left is little bit confusing. Imagine we are standing at the point where we are going to test. Look in the direction of the line we drew.

If the edge crosses the line from your right side to your left side, it's a counter-clockwise movement, so we add 1 to the winding number. If it crosses from our left side to our right side, it's a clockwise movement, so you subtract 1.

Interpreting the Winding Number

After counting the crossings and adding or subtracting from the winding number, we get our final result.

• Non-zero Winding Number − The point lies inside the polygon. This means the winding number can be any positive or negative number, but not zero.
• Zero Winding Number − The point lies outside the polygon.

Example of Non-zero Winding Number

Let us see the same polygon example from before. This time, we will use the Non-zero winding number method.

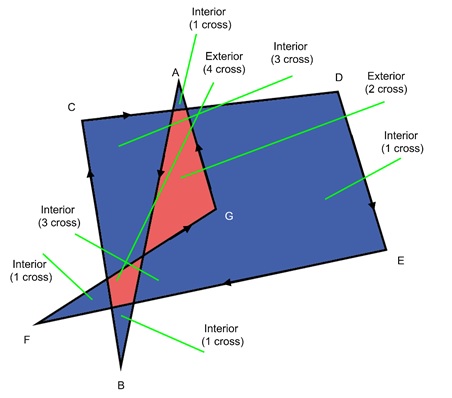
For example, let us consider point 'G'. Draw a line from 'G' to the outside. The initial winding number is 0. The first edge crosses from right to left (counter-clockwise), so we add 1 (winding number becomes 1). The second edge crosses from left to right (clockwise), so we subtract 1 (winding number becomes 0). The final winding number is 0, so point 'G' lies outside the polygon.

Now consider point 'A'. Draw a line from 'A' to the outside. The first edge crosses from right to left (counter-clockwise), so we add 1 (winding number becomes 1). There are no more edge crossings. The final winding number is 1, which is a non-zero value. Therefore, point 'A' lies inside the polygon.

We can apply this method to all the other points (B, C, D, E, and F) and verify if they are inside or outside the polygon.

Conclusion

In this chapter, we explained the Inside Outside Tests in Computer Graphics. We highlighted two methods, the Odd-Even rule and the Non-zero winding number method, to determine if a point lies inside or outside a polygon. We also discussed how to apply these rules and how to interpret the results. These tests are useful in different algorithms that require identifying interior regions of objects.