- Computer Graphics - Home
- Computer Graphics Basics
- Computer Graphics Applications
- Graphics APIs and Pipelines
- Computer Graphics Maths
- Sets and Mapping
- Solving Quadratic Equations
- Computer Graphics Trigonometry
- Computer Graphics Vectors
- Linear Interpolation
- Computer Graphics Devices
- Cathode Ray Tube
- Raster Scan Display
- Random Scan Device
- Phosphorescence Color CRT
- Flat Panel Displays
- 3D Viewing Devices
- Images Pixels and Geometry
- Color Models
- Line Generation
- Line Generation Algorithm
- DDA Algorithm
- Bresenham's Line Generation Algorithm
- Mid-point Line Generation Algorithm
- Circle Generation
- Circle Generation Algorithm
- Bresenham's Circle Generation Algorithm
- Mid-point Circle Generation Algorithm
- Ellipse Generation Algorithm
- Polygon Filling
- Polygon Filling Algorithm
- Scan Line Algorithm
- Flood Filling Algorithm
- Boundary Fill Algorithm
- 4 and 8 Connected Polygon
- Inside Outside Test
- 2D Transformation
- 2D Transformation
- Transformation Between Coordinate System
- Affine Transformation
- Raster Methods Transformation
- 2D Viewing
- Viewing Pipeline and Reference Frame
- Window Viewport Coordinate Transformation
- Viewing & Clipping
- Point Clipping Algorithm
- Cohen-Sutherland Line Clipping
- Cyrus-Beck Line Clipping Algorithm
- Polygon Clipping Sutherland–Hodgman Algorithm
- Text Clipping
- Clipping Techniques
- Bitmap Graphics
- 3D Viewing Transformation
- 3D Computer Graphics
- Parallel Projection
- Orthographic Projection
- Oblique Projection
- Perspective Projection
- 3D Transformation
- Rotation with Quaternions
- Modelling and Coordinate Systems
- Back-face Culling
- Lighting in 3D Graphics
- Shadowing in 3D Graphics
- 3D Object Representation
- Represnting Polygons
- Computer Graphics Surfaces
- Visible Surface Detection
- 3D Objects Representation
- Computer Graphics Curves
- Computer Graphics Curves
- Types of Curves
- Bezier Curves and Surfaces
- B-Spline Curves and Surfaces
- Data Structures For Graphics
- Triangle Meshes
- Scene Graphs
- Spatial Data Structure
- Binary Space Partitioning
- Tiling Multidimensional Arrays
- Color Theory
- Colorimetry
- Chromatic Adaptation
- Color Appearance
- Antialiasing
- Ray Tracing
- Ray Tracing Algorithm
- Perspective Ray Tracing
- Computing Viewing Rays
- Ray-Object Intersection
- Shading in Ray Tracing
- Transparency and Refraction
- Constructive Solid Geometry
- Texture Mapping
- Texture Values
- Texture Coordinate Function
- Antialiasing Texture Lookups
- Procedural 3D Textures
- Reflection Models
- Real-World Materials
- Implementing Reflection Models
- Specular Reflection Models
- Smooth-Layered Model
- Rough-Layered Model
- Surface Shading
- Diffuse Shading
- Phong Shading
- Artistic Shading
- Computer Animation
- Computer Animation
- Keyframe Animation
- Morphing Animation
- Motion Path Animation
- Deformation Animation
- Character Animation
- Physics-Based Animation
- Procedural Animation Techniques
- Computer Graphics Fractals
Computer Graphics Fractals
A French/American mathematician Dr Benoit Mandelbrot discovered Fractals. The word fractal was derived from a Latin word fractus which means broken.
What are Fractals in Computer Graphics?
Fractals are very complex pictures generated by a computer from a single formula. They are created using iterations. This means one formula is repeated with slightly different values over and over again, taking into account the results from the previous iteration.
Fractals are used in many areas such as −
Astronomy − For analyzing galaxies, rings of Saturn, etc.
Biology/Chemistry − For depicting bacteria cultures, Chemical reactions, human anatomy, molecules, plants,
Others − For depicting clouds, coastline and borderlines, data compression, diffusion, economy, fractal art, fractal music, landscapes, special effect, etc.

Generation of Computer Graphics Fractals
Fractals can be generated by repeating the same shape over and over again as shown in the following figure. In figure (a) shows an equilateral triangle. In figure (b), we can see that the triangle is repeated to create a star-like shape. In figure (c), we can see that the star shape in figure (b) is repeated again and again to create a new shape.
We can do unlimited number of iteration to create a desired shape. In programming terms, recursion is used to create such shapes.

Geometric Fractals
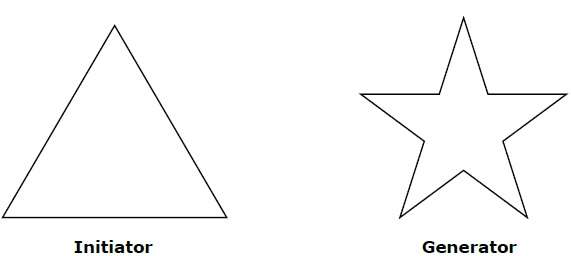
Geometric fractals deal with shapes found in nature that have non-integer or fractal dimensions. To geometrically construct a deterministic (nonrandom) self-similar fractal, we start with a given geometric shape, called the initiator. Subparts of the initiator are then replaced with a pattern, called the generator.
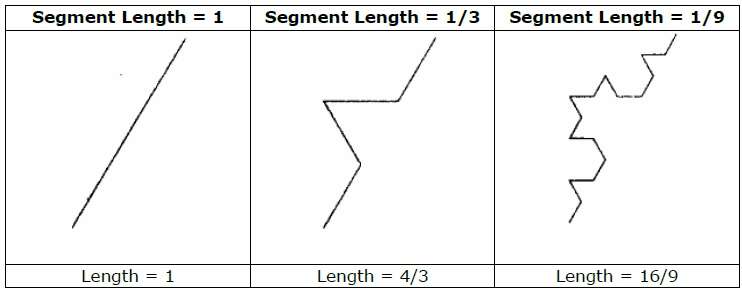
As an example, if we use the initiator and generator shown in the above figure, we can construct good pattern by repeating it. Each straight-line segment in the initiator is replaced with four equal-length line segments at each step. The scaling factor is 1/3, so the fractal dimension is D = ln 4/ln 3 ≈ 1.2619.
Also, the length of each line segment in the initiator increases by a factor of 4/3 at each step, so that the length of the fractal curve tends to infinity as more detail is added to the curve as shown in the following figure −