
- Computer Graphics - Home
- Computer Graphics Basics
- Computer Graphics Applications
- Graphics APIs and Pipelines
- Computer Graphics Maths
- Sets and Mapping
- Solving Quadratic Equations
- Computer Graphics Trigonometry
- Computer Graphics Vectors
- Linear Interpolation
- Computer Graphics Devices
- Cathode Ray Tube
- Raster Scan Display
- Random Scan Device
- Phosphorescence Color CRT
- Flat Panel Displays
- 3D Viewing Devices
- Images Pixels and Geometry
- Color Models
- Line Generation
- Line Generation Algorithm
- DDA Algorithm
- Bresenham's Line Generation Algorithm
- Mid-point Line Generation Algorithm
- Circle Generation
- Circle Generation Algorithm
- Bresenham's Circle Generation Algorithm
- Mid-point Circle Generation Algorithm
- Ellipse Generation Algorithm
- Polygon Filling
- Polygon Filling Algorithm
- Scan Line Algorithm
- Flood Filling Algorithm
- Boundary Fill Algorithm
- 4 and 8 Connected Polygon
- Inside Outside Test
- 2D Transformation
- 2D Transformation
- Transformation Between Coordinate System
- Affine Transformation
- Raster Methods Transformation
- 2D Viewing
- Viewing Pipeline and Reference Frame
- Window Viewport Coordinate Transformation
- Viewing & Clipping
- Point Clipping Algorithm
- Cohen-Sutherland Line Clipping
- Cyrus-Beck Line Clipping Algorithm
- Polygon Clipping Sutherland–Hodgman Algorithm
- Text Clipping
- Clipping Techniques
- Bitmap Graphics
- 3D Viewing Transformation
- 3D Computer Graphics
- Parallel Projection
- Orthographic Projection
- Oblique Projection
- Perspective Projection
- 3D Transformation
- Rotation with Quaternions
- Modelling and Coordinate Systems
- Back-face Culling
- Lighting in 3D Graphics
- Shadowing in 3D Graphics
- 3D Object Representation
- Represnting Polygons
- Computer Graphics Surfaces
- Visible Surface Detection
- 3D Objects Representation
- Computer Graphics Curves
- Computer Graphics Curves
- Types of Curves
- Bezier Curves and Surfaces
- B-Spline Curves and Surfaces
- Data Structures For Graphics
- Triangle Meshes
- Scene Graphs
- Spatial Data Structure
- Binary Space Partitioning
- Tiling Multidimensional Arrays
- Color Theory
- Colorimetry
- Chromatic Adaptation
- Color Appearance
- Antialiasing
- Ray Tracing
- Ray Tracing Algorithm
- Perspective Ray Tracing
- Computing Viewing Rays
- Ray-Object Intersection
- Shading in Ray Tracing
- Transparency and Refraction
- Constructive Solid Geometry
- Texture Mapping
- Texture Values
- Texture Coordinate Function
- Antialiasing Texture Lookups
- Procedural 3D Textures
- Reflection Models
- Real-World Materials
- Implementing Reflection Models
- Specular Reflection Models
- Smooth-Layered Model
- Rough-Layered Model
- Surface Shading
- Diffuse Shading
- Phong Shading
- Artistic Shading
- Computer Animation
- Computer Animation
- Keyframe Animation
- Morphing Animation
- Motion Path Animation
- Deformation Animation
- Character Animation
- Physics-Based Animation
- Procedural Animation Techniques
- Computer Graphics Fractals
Bresenham's Line Generation Algorithm
The DDA algorithm is good but it is not efficient enough due to its roundoff operations. As we know, Bresenham's algorithm is one of the most widely used techniques for this purpose. In this chapter, we will cover the Bresenham's Line Generation algorithm in detail and also highlight how it is different from the DDA algorithm.
Line Drawing Algorithm
A line drawing algorithm is a method used to display a line segment on discrete visual media, such as computer screens or printers with pixel-based resolution. These algorithms are important for creating graphics on digital devices.
The following two Line Drawing Algorithms are −
- DDA (Digital Differential Analyzer) Line Drawing Algorithm
- Bresenham Line Drawing Algorithm
There are other types of algorithms available, but these two are quite famous.
Bresenham's Line Drawing Algorithm
In previous articles we have seen this in detail. Here for a basic recap, the Bresenham's Line Drawing Algorithm is a technique used to draw straight lines on pixel-based displays like computer screens. It was first introduced by Jack E. Bresenham in 1962. It's widely used because it's both efficient and simple to implement.
The algorithm works by determining which pixels should be colored to create a close approximation of a straight line between two points. It uses only incremental integer calculations, making it fast and accurate.
How Does the Bresenham's Algorithm Work?
The algorithm works by making decisions about which pixels to plot based on the calculated error at each step. Here's a step-by-step breakdown of how it operates −
- Input − The algorithm takes the coordinates of two endpoints of the line as input.
- Calculation − It calculates the differences in x and y coordinates between the endpoints.
- Decision Parameter − The algorithm uses a decision parameter to determine which pixel to plot next.
- Pixel Selection − Based on the decision parameter, it chooses whether to move horizontally or diagonally to the next pixel.
- Update − The decision parameter is updated at each step.
- Repeat, steps 4 and 5 are repeated until the end point is reached.
Deriving the Bresenham's Algorithm
To understand how Bresenham's algorithm works, we need to look at its mathematical basis, since we have seen them in detail in the previous articles here we will see from an abstract view.
- Line Equation − The algorithm starts with the basic line equation: y = mx + b
- Sampling − It samples this continuous line at discrete x-coordinates (pixels).
- Error Calculation − At each step, it calculates the vertical distance between the ideal line and the nearest pixels above and below.
- Decision Making − The algorithm chooses the pixel closer to the ideal line.
- Efficient Implementation − Through clever algebraic manipulation, all calculations are done using only integer addition and subtraction.
Step-by-Step Algorithm
Here's a more detailed look at the steps of Bresenham's line drawing algorithm:
- Input the two endpoints of the line. Save the left endpoint as (x0, y0).
- Plot the first point (x0, y0).
- Calculate the constants Δx, Δy, 2Δy, and (2Δy - 2Δx).
- Calculate the initial decision parameter: p0 = 2Δy - Δx
- For each xk along the line, starting with k = 0:
- If pk < 0, plot (xk+1, yk) and set pk + 1 = pk + 2Δy
- Otherwise, plot (xk+1, yk+1) and set pk+1 = pk + 2Δy - 2Δx
- Repeat step 5 until you reach the end point.
Example
Let us take a look at an example to understand how this algorithm works.
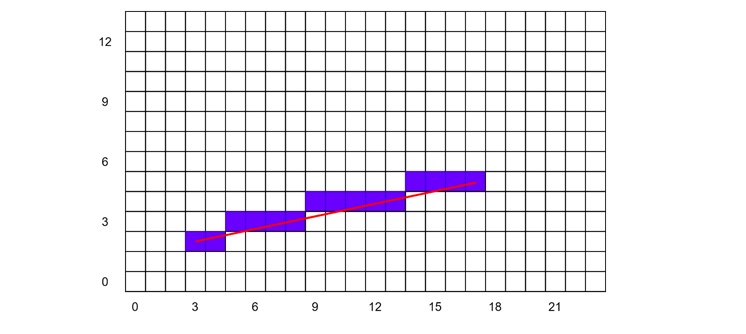
Consider the input points (3, 2) and (17, 5).
First, let's calculate our initial values −
- Δx = 17 - 3 = 14
- Δy = 5 - 2 = 3
- m = Δy / Δx = 3/14 (slope of the line)
- Initial decision parameter p = 2Δy - Δx = 2(3) - 14 = -8
Now, let's go through the algorithm step-by-step −
| Step | x | y | p | Plot Point | Next Action |
|---|---|---|---|---|---|
| 0 | 3 | 2 | -8 | (3, 2) | x = x + 1, p = p + 2y |
| 1 | 4 | 2 | -2 | (4, 2) | x = x + 1, p = p + 2y |
| 2 | 5 | 2 | 4 | (5, 3) | x = x + 1, y = y + 1, p = p + 2y - 2x |
| 3 | 6 | 3 | -10 | (6, 3) | x = x + 1, p = p + 2y |
| 4 | 7 | 3 | -4 | (7, 3) | x = x + 1, p = p + 2y |
| 5 | 8 | 3 | 2 | (8, 3) | x = x + 1, y = y + 1, p = p + 2y - 2x |
| 6 | 9 | 4 | -12 | (9, 4) | x = x + 1, p = p + 2y |
| 7 | 10 | 4 | -6 | (10, 4) | x = x + 1, p = p + 2y |
| 8 | 11 | 4 | 0 | (11, 4) | x = x + 1, p = p + 2y |
| 9 | 12 | 4 | 6 | (12, 4) | x = x + 1, y = y + 1, p = p + 2y - 2x |
| 10 | 13 | 5 | -8 | (13, 4) | x = x + 1, p = p + 2y |
| 11 | 14 | 5 | -2 | (14, 5) | x = x + 1, p = p + 2y |
| 12 | 15 | 5 | 4 | (15, 5) | x = x + 1, y = y + 1, p = p + 2y - 2x |
| 13 | 16 | 5 | -10 | (16, 5) | x = x + 1, p = p + 2y |
| 14 | 17 | 5 | -4 | (17, 5) | End |
Advantages of Bresenham's Line Drawing Algorithm
Following are the Advantages of Bresenham's Line Drawing Algorithm −
- Simplicity − The algorithm is easy to understand and implement.
- Efficiency − It uses only integer arithmetic, making it fast.
- Versatility − We can use it to draw lines in any direction.
- Hardware Implementation − It is suitable for hardware implementation due to its use of simple arithmetic operations.
Disadvantages of Bresenham's Line Drawing Algorithm
Following are the disadvantages of Bresenham's Line Drawing Algorithm –
- Limited Smoothness − The resulting line may not be as smooth as desired, especially for short lines.
- Fixed Line Thickness − The algorithm only draws one-pixel-thick lines.
Comparison with DDA Algorithm
Bresenham's algorithm has several advantages over the Digital Differential Analyzer (DDA) algorithm:
- Operations − Bresenham's algorithm uses only addition and subtraction, while DDA uses multiplication and division.
- Precision − Bresenham's algorithm is more precise and accurate.
- Calculation Complexity − Bresenham's algorithm uses simpler calculations than roundoff in DDA.
- Efficiency − Bresenham's algorithm is more efficient overall.
- Optimization − Bresenham's algorithm allows for optimization, while DDA does not.
Conclusion
In this chapter, we covered the Bresenham's Line Drawing Algorithm. We explained its basic concept, how it works, and provided a step-by-step breakdown of the algorithm.