
- Computer Graphics - Home
- Computer Graphics Basics
- Computer Graphics Applications
- Graphics APIs and Pipelines
- Computer Graphics Maths
- Sets and Mapping
- Solving Quadratic Equations
- Computer Graphics Trigonometry
- Computer Graphics Vectors
- Linear Interpolation
- Computer Graphics Devices
- Cathode Ray Tube
- Raster Scan Display
- Random Scan Device
- Phosphorescence Color CRT
- Flat Panel Displays
- 3D Viewing Devices
- Images Pixels and Geometry
- Color Models
- Line Generation
- Line Generation Algorithm
- DDA Algorithm
- Bresenham's Line Generation Algorithm
- Mid-point Line Generation Algorithm
- Circle Generation
- Circle Generation Algorithm
- Bresenham's Circle Generation Algorithm
- Mid-point Circle Generation Algorithm
- Ellipse Generation Algorithm
- Polygon Filling
- Polygon Filling Algorithm
- Scan Line Algorithm
- Flood Filling Algorithm
- Boundary Fill Algorithm
- 4 and 8 Connected Polygon
- Inside Outside Test
- 2D Transformation
- 2D Transformation
- Transformation Between Coordinate System
- Affine Transformation
- Raster Methods Transformation
- 2D Viewing
- Viewing Pipeline and Reference Frame
- Window Viewport Coordinate Transformation
- Viewing & Clipping
- Point Clipping Algorithm
- Cohen-Sutherland Line Clipping
- Cyrus-Beck Line Clipping Algorithm
- Polygon Clipping Sutherland–Hodgman Algorithm
- Text Clipping
- Clipping Techniques
- Bitmap Graphics
- 3D Viewing Transformation
- 3D Computer Graphics
- Parallel Projection
- Orthographic Projection
- Oblique Projection
- Perspective Projection
- 3D Transformation
- Rotation with Quaternions
- Modelling and Coordinate Systems
- Back-face Culling
- Lighting in 3D Graphics
- Shadowing in 3D Graphics
- 3D Object Representation
- Represnting Polygons
- Computer Graphics Surfaces
- Visible Surface Detection
- 3D Objects Representation
- Computer Graphics Curves
- Computer Graphics Curves
- Types of Curves
- Bezier Curves and Surfaces
- B-Spline Curves and Surfaces
- Data Structures For Graphics
- Triangle Meshes
- Scene Graphs
- Spatial Data Structure
- Binary Space Partitioning
- Tiling Multidimensional Arrays
- Color Theory
- Colorimetry
- Chromatic Adaptation
- Color Appearance
- Antialiasing
- Ray Tracing
- Ray Tracing Algorithm
- Perspective Ray Tracing
- Computing Viewing Rays
- Ray-Object Intersection
- Shading in Ray Tracing
- Transparency and Refraction
- Constructive Solid Geometry
- Texture Mapping
- Texture Values
- Texture Coordinate Function
- Antialiasing Texture Lookups
- Procedural 3D Textures
- Reflection Models
- Real-World Materials
- Implementing Reflection Models
- Specular Reflection Models
- Smooth-Layered Model
- Rough-Layered Model
- Surface Shading
- Diffuse Shading
- Phong Shading
- Artistic Shading
- Computer Animation
- Computer Animation
- Keyframe Animation
- Morphing Animation
- Motion Path Animation
- Deformation Animation
- Character Animation
- Physics-Based Animation
- Procedural Animation Techniques
- Computer Graphics Fractals
Triangle Meshes in Computer Graphics
Triangle meshes are a type of advanced data structure that are needed to represent 3D surfaces efficiently. These meshes are made up of triangles that share vertices, edges, and form continuous surfaces. Handling them efficiently is important in several applications, including rendering, texture mapping, and animation.
In this chapter, we will see the basics of triangle meshes, their topology, data storage formats, and the methods used for processing these meshes.
Basic Structure of a Triangle Mesh
To represent a triangle mesh, the minimum information needed is a set of triangles and the positions of their vertices in 3D space. However, many programs also need to store additional information at the vertices, edges, or faces.
For example, each vertex may have data like texture coordinates, material properties, or lighting parameters. This information is then linearly interpolated across the triangles to create smooth transitions across the mesh.
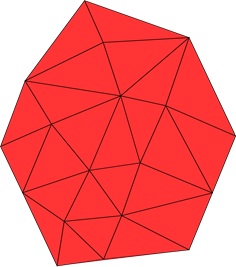
Vertices are commonly shared between triangles, and this sharing reduces the amount of memory required to store the mesh. Without this shared structure, every triangle would need its own set of vertices, increasing memory consumption and bandwidth usage when transmitting meshes across networks or from the CPU to the GPU.
Mesh Topology
The organization of triangles in a mesh is referred to as its topology. In most cases, graphics algorithms work best with meshes that have predictable connectivity. One common requirement is that the mesh must be a manifold, which means that the mesh is “watertight” and looks like a smooth surface everywhere.
To ensure a mesh is manifold, it must meet two basic conditions:
- Every edge is shared by exactly two triangles.
- Every vertex connects to a single loop of triangles.
If an edge is shared by more than two triangles, or if a vertex connects to multiple loops of triangles, the mesh is considered non-manifold. Non-manifold meshes can cause issues in algorithms. This may lead to crashes or incorrect outputs.
In some cases, it is necessary to allow for non-manifold edges or vertices, particularly when working on surfaces that have boundaries. These are called manifolds with boundaries. These meshes are not watertight, but they are often acceptable in graphics applications.
Example: Non-Manifold vs Manifold Meshes
Non-manifold edges and vertices are best understood through examples. Consider an edge shared by three triangles. The extra triangle creates a "fin," causing the edge to fail the manifold condition. Similarly, if multiple disconnected sets of triangles share the same vertex, the vertex fails the manifold condition.
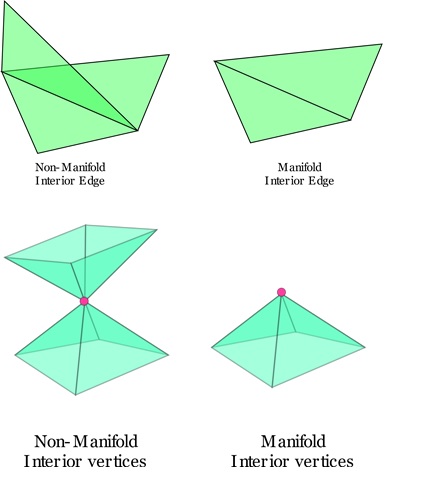
In contrast, a manifold mesh will have every edge shared by exactly two triangles, and every vertex will be part of a single connected loop of triangles. This ensures that the surface can be smoothed and processed consistently by graphics algorithms.
Indexed Mesh Storage
A basic triangle mesh can be stored by listing the three vertices of each triangle. However, this approach may have duplication of vertices. For example, if a vertex is shared by multiple triangles, it must be stored multiple times, once for each triangle. A better approach is to use indexed mesh storage, where each unique vertex is stored once, and triangles reference these shared vertices.
In an indexed mesh, the triangles are defined using indices that point to the shared vertices. This reduces the overall storage requirement. For example, in a mesh with four unique vertices and three triangles, storing each triangle independently would require nine vertices in total. With indexed storage, only four vertices are needed, along with the indices for the triangles.
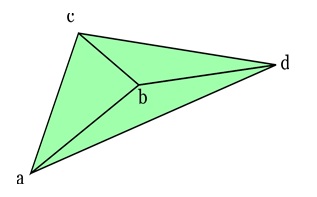
This storage method is called an indexed triangle mesh and is widely used in computer graphics because it is both space-efficient and simple to implement.
Example: Indexed Mesh vs Separate Triangles
Consider a simple triangle mesh with three triangles and four vertices. Storing each triangle separately would result in nine stored vertices, as each triangle would store its own set of vertices.
Using an indexed mesh allows us to store only four unique vertices. The triangles then reference these shared vertices by their indices. This reduces storage requirements significantly without affecting the structure of the mesh.
| Triangle | Vertices | ||
|---|---|---|---|
| Index | Vertices | Index | Positions |
| 0 | (0, 1, 2) | 0 | (ax, ay, az) |
| 1 | (1, 3, 2) | 1 | (bx, by, bz) |
| 2 | (0, 3, 1) | 2 | (cx, cy, cz) |
| 3 | (dx, dy, dz) | ||
Triangle Strips and Fans
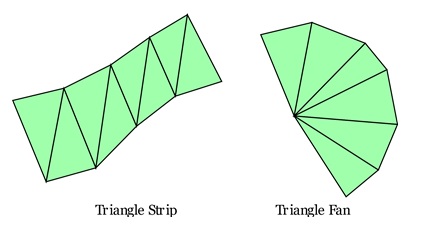
When even more compact storage is needed, triangle strips and triangle fans can be used. These methods reduce the amount of space required to store the vertex indices of a mesh. In a triangle strip, vertices are added in a linear sequence, alternating between the top and bottom of the strip. Each new vertex creates a new triangle using the two most recent vertices in the sequence.
In a triangle fan, all triangles share a common vertex, and the remaining vertices form a fan-like structure. This reduces the number of vertex indices that need to be stored, especially when compared to a standard indexed mesh.
Example of Triangle Fan and Strip
A triangle fan might include a central vertex connected to several surrounding vertices. Instead of storing the full list of vertex indices for each triangle, the fan is described by a single vertex and a sequence of adjacent vertices. Similarly, in a triangle strip, each new triangle shares two vertices with the previous triangle, so the mesh can be described with far fewer vertex indices than a traditional mesh.
Mesh Connectivity
For static meshes, indexed meshes, triangle strips, and fans these are effective storage methods. However, when meshes need to be edited or modified, more complex data structures are necessary. Efficiently editing meshes requires answering questions like:
- Which triangles are adjacent to a given triangle?
- Which triangles share a specific edge or vertex?
To handle these queries efficiently, data structures can be designed that store some of the connectivity information directly. One such structure is the triangle-neighbour structure, where each triangle stores references to its three neighbouring triangles and its three vertices.
Example of Triangle-Neighbor Structure
In a triangle-neighbour structure, each triangle contains references to its neighbouring triangles and vertices. This allows for efficient traversal of the mesh to answer queries about the relationships between triangles and vertices.
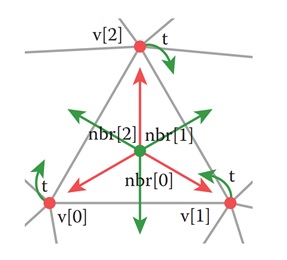
This structure is particularly useful when performing operations like mesh subdivision or simplification, where the relationships between triangles and vertices are critical.
Conclusion
In this chapter, we covered the basics of triangle meshes in computer graphics. Starting with the structure of a triangle mesh, we explained the importance of shared vertices and efficient storage methods like indexed meshes. We then examined mesh topology and the concept of manifold meshes, followed by examples of non-manifold and manifold configurations.
Additionally, we looked at indexed mesh storage and how triangle strips and fans can reduce storage requirements. Finally, we covered advanced data structures like the triangle-neighbour structure for handling mesh connectivity and editing.